Nội suy là phương pháp được sử dụng phổ biến bởi nhà khoa học, kỹ sư, nhiếp ảnh gia và nhà toán học,…Vậy nội suy là gì? Công thức nội suy tuyến tính 1 chiều, 2 chiều là gì? Cùng Palada.vn tìm hiểu và phân tích qua các ví dụ cụ thể nhé!
Tóm tắt
Nội suy là gì?
Có rất nhiều định nghĩa để giải thích cho khái niệm nội suy là gì, phương pháp nội suy là gì. Nội suy là phương pháp sử dụng để ước tính giá trị tại các điểm dữ liệu chưa biết trong phạm vi của một tập hợp rời rạc chứa một số dữ liệu đã biết trước đó.

Trong khoa học kỹ thuật, có một số điểm dữ liệu đã biết được giá trị bằng cách lấy mẫu thí nghiệm. Các điểm này sẽ là giá trị của 1 hàm số của biến số độc lập có lượng giới hạn giá trị. Thông thường, chúng ta phải nội suy hoặc ước tính giá trị hàm số này với giá trị trung gian của biến số độc lập. Nó được thực hiện bằng phương pháp phân tích hồi quy.
Phương pháp nội suy để làm gì?
Nội suy là công cụ toán học được ứng dụng trong rất nhiều lĩnh vực, ngành nghề khác nhau như công thức nội suy trong xây dựng, công nghệ thông tin, dầu khí, điện ảnh hay tài chính,…
Trong một số trường hợp tính toán dữ liệu, khi mà đầu vào không phải là một con số cụ thể mà là khoảng giá trị từ A đến B. Khi đó, chúng ta không thể lấy A hoặc B làm giá trị đại diện mà cần phải sử dụng số liệu của đề bài để lựa chọn giá trị N trong khoảng (A, B) để có kết quả chính xác nhất.
Phương pháp nội suy

Có nhiều loại phương pháp nội suy khác nhau như:
- Phương pháp nội suy tuyến tính – áp dụng một đa thức tuyến tính riêng biệt giữa mỗi cặp điểm dữ liệu cho đường cong hoặc trong bộ 3 điểm cho bề mặt.
- Phương pháp lân cận gần nhất – chèn giá trị của một điểm được nội suy vào giá trị của điểm dữ liệu liền kề nhất. Do đó, phương pháp này không tạo ra bất kỳ điểm dữ liệu mới nào.
- Phương pháp nội suy Spline khối – phù hợp với 1 đa thức khối khác nhau giữa mỗi cặp điểm dữ liệu cho đường cong hoặc giữa bộ 3 điểm cho bề mặt.
- Phương pháp bảo quản hình dạng – còn được gọi là phương pháp nội suy Hermite khối (PCHIP). Nó bảo toàn tính đơn điệu và dạng của dữ liệu và chỉ dành cho các đường cong.
- Phương pháp Spline bản mỏng – bao gồm các bề mặt nhẵn cũng có thể ngoại suy tốt và chỉ dành cho bề mặt
- Phương pháp nội suy Biharmonic – chỉ được áp dụng cho các bề mặt.
Công thức tính nội suy
Cách tính nội suy giá trị trung bình của hàm F(x) gần bằng đường thẳng r(x). Có nghĩa là hàm thay đổi tuyến tính với “x” cho đoạn “x=a” và “x=b”; Đối với giá trị “x” trong khoảng từ (X0, X1) và (0, 1) giá trị của y được cho bởi khoảng giữa các điểm và được biểu thị bằng mối quan hệ như sau:
(Và – Và 0) ÷ (X – X0) = (Và 1 – Và 0) ÷ (X1 – X0)
Để đây là phép nội suy tuyến tính, điều kiện cần thiết là đa thức nội suy là bậc một (n = 1), để nó điều chỉnh theo các giá trị x0 và x1.
Phép nội suy tuyến tính dựa trên sự giống nhau của các tam giác. Do đó xuất phát từ hình học trước đó; ta có thể nhận được giá trị của “y”, đại diện cho giá trị chưa biết cho “x”.
Phương pháp nội suy tuyến tính
Nội suy tuyến tính là gì?
Nội suy tuyến tính là một phương pháp cho phép bạn suy ra 1 giá trị giữa 2 giá trị được xác định rõ, có thể nằm trong một bảng hoặc trong biểu đồ tuyến tính.
Nội suy tuyến tính là một phương pháp bắt nguồn từ phép nội suy tổng quát của Newton. Phương pháp này được xác định bằng cách xấp xỉ một giá trị không xác định nằm giữa 2 số đã cho. Đó là, có 1 giá trị trung gian. Nó cũng được áp dụng cho các hàm gần đúng.
Có nhiều loại nội suy khác nhau, như các lớp tuyến tính, bậc hai, khối và cao hơn, đơn giản nhất là xấp xỉ tuyến tính. Tuy nhiên, nhược điểm của phép nội suy tuyến tính là kết quả sẽ không chính xác như xấp xỉ bởi các hàm của các lớp cao hơn.
Ví dụ: nếu bạn biết rằng 3 lít sữa có giá bán 4 đô la và 5 lít sữa có giá bán 7 đô la, nhưng bạn muốn biết giá bán của 4 lít sữa là bao nhiêu. Lúc này, ta có thể dùng phương pháp nội suy bằng tay để xác định giá trị trung gian đó.
Nội suy tuyến tính 1 chiều
Đây là phương pháp nội suy chỉ có 2 kiểu dữ liệu. Ta dựa vào dữ liệu 1 để suy ra giá trị kiểu 2 và ngược lại.
Ví dụ:
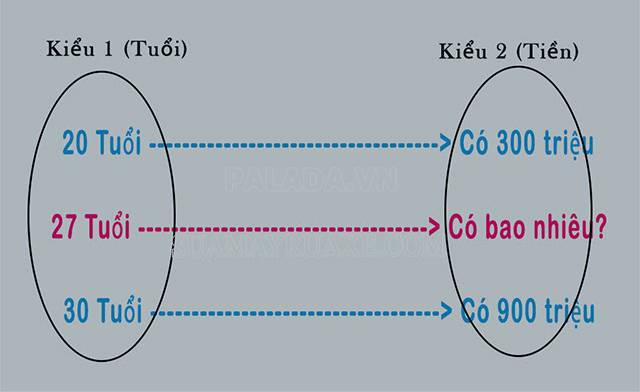
Cách tính:
Gọi số tiền mình có được năm 27 tuổi là X thì lúc đó ta có công thức nội suy như sau: (27 – 20)/(30 – 27) = (X – 300)/(900 – X)
Sau khi giải ra X = 720 triệu
Vậy khi bạn 27 tuổi, bạn sẽ có 720 triệu đồng.
Xác định chiều dòng điện cảm ứng – Các bước xác định, quy tắc
Tính chất đường trung trực của tam giác, định nghĩa và bài tập
Nội suy tuyến tính 2 chiều
Phương pháp này có vẻ rắc rối hơn nội suy 1 chiều. Nhưng nó vẫn đơn giản nếu bạn để ý kỹ. Với loại này sẽ có tổng cộng 3 kiểu dữ liệu. Và các bạn chỉ đi tìm giá trị của một dữ liệu tại hai giá trị xác định của 2 kiểu dữ liệu kia.
Ví dụ:
| Tiền bố mẹ cho | 300 | 400 | 900 |
| Tuổi | |||
| 20 | 70 | X1 | 100 |
| 25 | X2 | ||
| 30 | 100 | X3 | 140 |
Khi bạn 20 tuổi bố mẹ cho bạn 300 triệu thì bạn mua được 70kg hàng bán. Nếu bố mẹ cho 900 triệu thì bạn mua được 100kg. Đến lúc bạn 30 tuổi bố mẹ cho 300 triệu thì bạn lấy được 100kg hàng; còn 900 triệu thì lấy được 140kg. Vậy khi bạn 25 tuổi, bố mẹ cho 400 triệu thì bạn mua được bao nhiêu hàng hóa?
Cách giải:
Mục tiêu của chúng ta là tìm được X2, nhưng trước hết phải tính được X1 và X3.
Ta có: (400 – 300)/(900 – 400) = (X1- 70)/(100 – X1)
⇒ X1 = 75
Tương tự: (400 – 300)/(900 – 400) = (X3 – 100)/(140 – X3)
⇒ X3 = 106.667
Bây giờ sẽ tính X2
(25 – 20)/(30 – 25) = (X2 – 75)/(106.667 – X2)
⇒ X2 = 90.8
Vừa rồi, bài viết đã giải thích nội suy là gì? Công thức nội suy tuyến tính 1 chiều, 2 chiều cùng những ví dụ thực tế vô cùng dễ hiểu. Hy vọng những kiến thức mà Palada.vn vừa cung cấp sẽ giúp bạn áp dụng vào giải các bài tập liên quan đến phép nội suy được dễ dàng và chính xác hơn.



