Trong hệ trục tọa độ có trục tung và trục hoành. Trục tung là gì? Trục hoành là gì? Trục hoành, trục tung là ngang hay dọc? Cùng Palada.vn ôn lại kiến thức về trục tung và trục hoành nhé.
Tóm tắt
Tìm hiểu về hệ trục tọa độ
Định nghĩa: Hệ trục tọa độ Oxy gồm có 2 trục tung và trục hoành vuông góc với nhau.
Trong đó
- O: gốc tọa độ
- Ox: trục hoành (còn gọi là hoành độ)
- Oy: trục tung (còn gọi là tung độ)
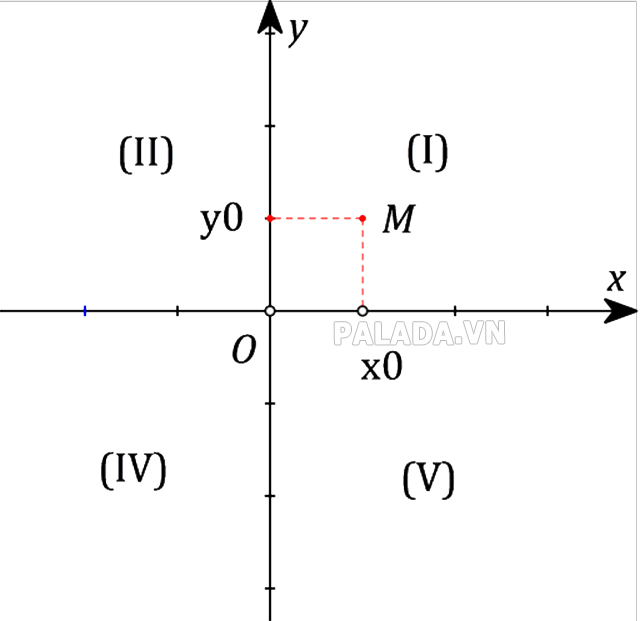
– Trục tọa độ là đường thẳng mà trên đó đã xác định 1 điểm gốc O và 1 vectơ đơn vị
– Mặt phẳng chứa hệ trục tọa độ Oxy đc gọi là mặt phẳng tọa độ Oxy.
– Hai vectơ bằng nhau khi các tọa độ tương ứng giống nhau
– Tọa độ của vectơ = tọa độ của điểm ngọn – tọa độ tương ứng của điểm đầu.
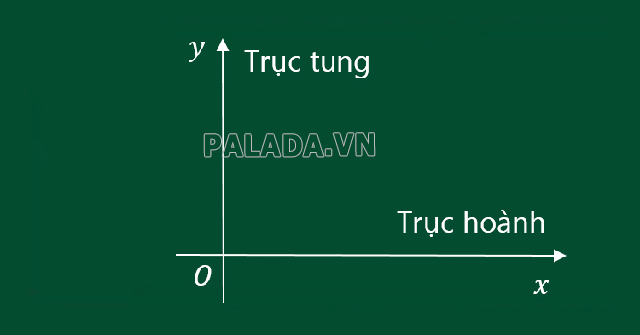
Trục tung, trục hoành là gì?
Hệ tọa độ Oxy gồm 2 trục:
- Trục tung là ngang hay dọc? Trục tung là trục dọc dựng thẳng đứng
- Trục hoành là trục nằm ngang.
Người ta ghi nhớ trục tung và trục hoành bằng câu nói “Hoành ngang, tung dọc”
– Đặc điểm tọa độ của một điểm bất kỳ trong mặt phẳng tọa độ Oxy:
+ Trên mặt phẳng tọa độ, mỗi điểm A xác định một cặp (x0; y0). Ngược lại, mỗi cặp (x0; y0) xác định vị trí của một điểm A. Kí hiệu A(x; y)
+ Cặp số (x0; y0) gọi là toạ độ của điểm A; trong đó, x0 là hoành độ còn y0 là tung độ của điểm A.
Chú ý:
- Bao giờ cũng viết tọa độ của hoành độ trước, rồi tung độ sau.
- Toạ độ điểm gốc O là (0; 0).
Vai trò của trục tung và trục hoành trong việc xác định vị trí của điểm trên mặt phẳng?
Trục tung và trục hoành là 2 trục trong hệ tọa độ Oxy dùng để xác định vị trí của điểm trên mặt phẳng.
Vai trò của trục tung là gì?
Trục tung (trục nằm dọc) là một đường thẳng đứng, nằm song song với trục Oy. Trục tung được sử dụng để xác định chiều cao của một điểm bất kỳ trên mặt phẳng.
Trục tung là Ox hay Oy? Trục tung là trục Oy
Vai trò của trục hoành là gì?
Trục hoành (trục nằm ngang) là một đường thẳng nằm song song với trục Ox. Trục hoành được dùng để xác định chiều rộng hoặc chiều dài của một điểm bất kỳ trên mặt phẳng.
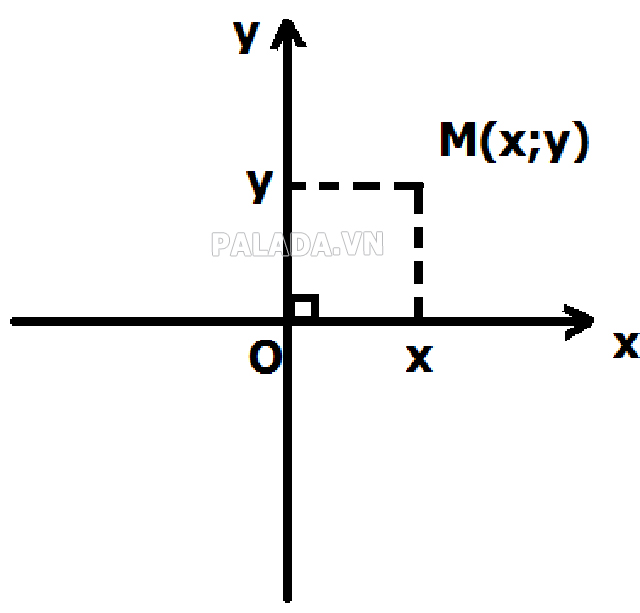
Khi xác định vị trí của 1 điểm bất kỳ trong mặt phẳng hệ tọa độ Oxy, chúng ta sẽ dóng cho điểm đó một cặp số tương ứng với tọa độ trên trục tung và trục hoành. Số đầu tiên trong cặp số chính là tọa độ trục hoành và số thứ hai là tọa độ trục tung.
Ví dụ: Nếu một điểm có tọa độ (7, 9), điểm này nằm ở phía bên phải 7 đơn vị và phía trên 9 đơn vị so với gốc O (vị trí gốc của hệ trục tọa độ Oxy).
Từ đó, ta có thể xác định được vị trí các điểm trên mặt phẳng Oxy bằng cách chỉ ra tọa độ 2 trục trục tung và trục hoành của chúng. Qua đó, trục tung và trục hoành chính là công cụ giúp chúng ta xác định được vị trí của điểm trên mặt phẳng hệ tọa độ Oxy.
Làm sao để xác định được tọa độ trục tung và trục hoành của điểm?
Để xác định trục tung và trục hoành trong mặt phẳng tọa độ Oxy, ta cần quan sát các đặc điểm sau:
1. Trục tung là trục dọc thẳng trên mặt phẳng toạ độ.
2. Trục hoành là trục nằm ngang trên mặt phẳng toạ độ.
3. Trục tung và trục hoành cắt nhau tại điểm gốc O của hệ tọa độ.
Ví dụ: Trong hệ tọa độ Oxy, trục tung chính là trục dọc Oy còn trục hoành sẽ là trục ngang Ox.
Để xác định trục tung và trục hoành, ta sử dụng các thông tin cung cấp trong đề bài hoặc sử dụng công thức tính và quy tắc định nghĩa về hệ tọa độ.
Bài tập về trục tung và trục hoành
Tìm trên mặt phẳng toạ độ Oxy, tìm tất cả các điểm có:
Hoành độ bằng 0. Tung độ bằng 0.
Hoành độ bằng 1. Tung độ bằng -4.
Hoành độ bằng số đối của tung độ.
Hoành độ bằng tung độ.
Hướng dẫn giải
- Tất cả các điểm đều cùng nằm trên trục tung Oy.
- Tất cả các điểm đều nằm trên trục hoành Ox.
- Tất cả các điểm đều nằm trên đường thẳng song song vs trục tung và cắt trục hoành tại điểm 1.
- Tất cả các điểm đều nằm trên đường thẳng song song vs trục hoành và cắt trục tung tại điểm -4.
- Tất cả các điểm đều nằm trên đường thẳng chứa tia phân giác của góc phần tư II và IV.
- Tất cả các điểm đều nằm trên đường thẳng chứa tia phân giác của góc phần tư I và III.
Công thức tính góc giữa 2 vecto, cách xác định nhanh, đơn giản
Với nội dung kiến thức tổng hợp về khái niệm trục tung và trục hoành trên đây, hẳn bạn đã hiểu thế nào là trục tung và trục hoành, chúng có vai trò như thế nào trong hệ trục tọa độ. Khi giải bài tập, cần xác định chính xác tọa độ của điểm để viết phương trình trục tung, trục hoành sao cho chính xác.



