Số thuần ảo hay số phức thuần ảo đặc biệt hữu ích trong các bài toán liên quan đến tương tác giữa các thông số có phần ảo; được ứng dụng trong thực tế ngành công nghiệp điện tử, sóng điện từ và nhiều lĩnh vực khác. Vậy Số thuần ảo là gì? Số phức nào là số thuần ảo? Palada.vn sẽ giải đáp những thắc mắc về số thuần ảo qua bài viết sau đây.
Tóm tắt
Số phức là gì?
- Số phức được biểu diễn dưới dạng z=a+bi. Trong đó, a và b là các số nguyên (Z). Số a chính là phần thực của số phức, số b là phần ảo của số phức. Còn giá trị i được xem là đơn vị ảo, quy ước i2 = – 1.

- Tập hợp số phức này được ký hiệu là C.
- Nếu z là số thực thì phần ảo b có giá trị bằng 0. Ngược lại, nếu z là số thuần ảo thì giá trị a (phần thực của z) là 0.
- Xét hai số phức z = a + bi và z’ = a’ + b’i. Điều kiện để 2 số phức này bằng nhau ⇔ a=a’; b=b’
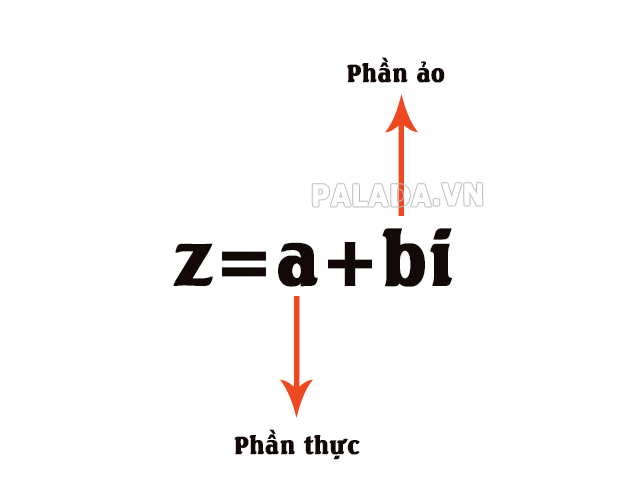
Số thuần ảo là gì?
Số thuần ảo là 1 dạng của số phức. Khi số phức Z có phần thực a = 0 thì Z = bi sẽ thuộc R => Z lúc này sẽ là ví dụ số thuần ảo.
Ví dụ bài tập số thuần ảo: Tìm số thuần ảo. Số phức nào dưới đây là số thuần ảo?
- z = -2 + 3i
- z = 3i
- z = -2
- √z = √3 + i
=> Đáp án B
Số ảo z = a + bi là số thuần ảo nếu a = 0 và b ≠0
Do đó, z = 3i là số thuần ảo.
Số phức thuần ảo là gì?
Số phức thuần ảo là loại số phức đặc biệt, trong đó phần thực của số
phức bằng 0 và chỉ có phần ảo. Nó có dạng biểu diễn là bi*i, trong đó “bi”
là một số thực bất kỳ và “i” là một đơn vị ảo trong toán học, với tính chất cơ
bản là i^2 = -1

Ví dụ: Tính giá trị của biểu thức và biểu diễn kết quả dưới dạng số phức thuần ảo: (3i)^2 – 4i + 2
Giải: Chúng ta thực hiện các phép tính theo thứ tự và biểu diễn kết quả dưới dạng số phức thuần ảo.
- Tính (3i)^2:
(3i)^2 = 3^2 * i^2 = 9 * (-1) = -9
- Tính -4i:
Tính tổng của các kết quả:
(-9) – 4i + 2 = -9 – 4i + 2 = -7 – 4i
Kết quả của biểu thức là -7 – 4i, n. Trong đó -7 là phần thực và -4i là phần ảo của số phức thuần ảo này.
Vậy, giá trị của biểu thức (3i)^2 – 4i + 2 là -7 – 4i.
Giai thừa là gì? Công thức tính giai thừa trong Toán học và ví dụ
Z là tập hợp số gì? Z là gì trong toán học? Bài tập minh họa
Ý nghĩa số phức thuần ảo
Số phức thuần ảo có ý nghĩa quan trọng trong nhiều lĩnh vực đời sống như toán học, khoa học và kỹ thuật. Dưới đây là một số ý nghĩa phổ biến của số phức thuần ảo:
- Biểu diễn tương tác phức tạp: Số phức thuần ảo sử dụng để mô tả các tương tác hoặc hiện tượng có phần ảo mà không có phần thực. Ví dụ, trong được biểu diễn bằng số phức thuần ảo để mô phỏng tương tác giữa dòng điện và từ trường.
- Điện tử và kỹ thuật điện tử: Số phức thuần ảo được ứng dụng rộng rãi trong kỹ thuật điện tử để mô tả các thông số như điện áp, dòng điện trong mạch điện. Điều này giúp thiết kế và phân tích mạch điện tử phức tạp.
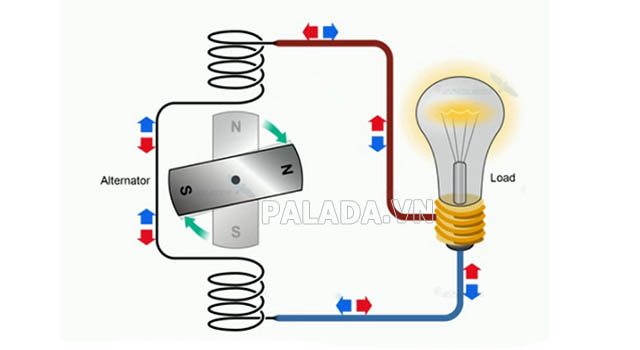
- Sóng âm thanh và sóng điện từ: Trong khoa học nghiên cứu sóng âm thanh và sóng điện từ, số phức thuần ảo dùng để biểu diễn sóng dừng và sóng phản xạ. Nó giúp mô tả tần số, biên độ và pha của sóng.
- Khoa học lượng tử: Trong lĩnh vực khoa học lượng tử, số phức thuần ảo mô tả trạng thái lượng tử của các hệ thống, như trạng thái sóng hệ thống và trạng thái năng lượng của hạt.
- Cơ học dòng chảy: Trong cơ học dòng chảy, số phức thuần ảo được sử dụng để mô tả áp suất dòng chảy trong các mô hình phức tạp của dòng chảy.
- Kỹ thuật ứng dụng: Số phức thuần ảo được ứng dụng rộng rãi trong các ứng dụng kỹ thuật như xử lý tín hiệu, điện tử và công nghiệp điện lạnh.
Với những thông tin giải thích số phức thuần ảo là gì mà bài viết vừa cung cấp, có thể thấy rằng số phức thuần ảo là một công cụ mạnh mẽ để biểu diễn và xử lý thông tin trong những tình huống phức tạp. Nó có nhiều ứng dụng quan trọng trong khoa học và công nghệ. Bởi vậy, hiểu được ý nghĩa của số phức thuần ảo sẽ giúp ngành khoa học công nghệ có những bước tiến vượt trội trong tương lai.



