Điểm đối xứng là một trong những vị trí điểm có ý nghĩa đặc biệt trong Toán hình học lớp 12. Vậy, điểm đối xứng là gì? Cách tìm điểm đối xứng qua đường thẳng như thế nào? Cùng Palada.vn tìm hiểu qua bài viết sau đây nhé.
Tóm tắt
Điểm đối xứng là gì?
2 điểm đối xứng qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối 2 điểm đó.
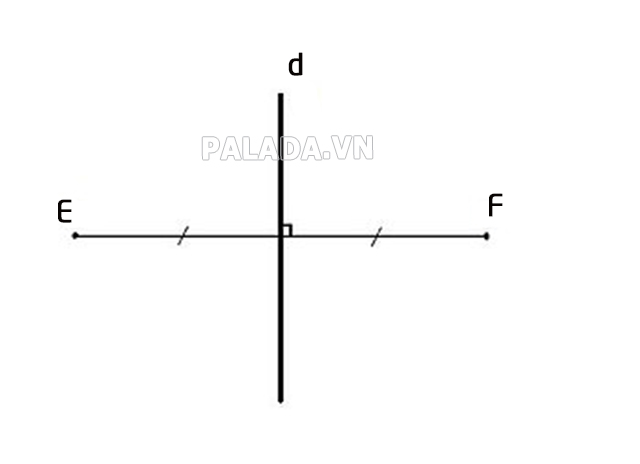
Ví dụ: Cho điểm E đối xứng với điểm F qua đường thẳng d thì d là đường trung trực của đoạn thẳng EF.
Quy ước: Nếu điểm E nằm trên đường thẳng d thì điểm đối xứng với B qua đường thẳng d cũng là điểm E.
Cách tìm điểm đối xứng qua đường thẳng
- Cách giải 1:
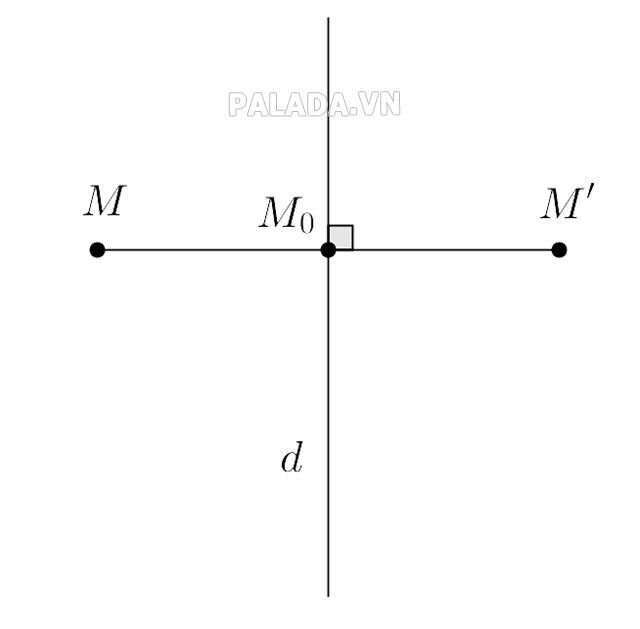
Giải sử, cần tìm điểm M’ đối xứng với điểm M qua đường thẳng (d), ta làm như sau:
– Tìm hình chiếu H của điểm M trên đường thẳng (d).
– M’ đối xứng với điểm M qua đường thẳng (d) nên M’ đối xứng với điểm M qua H (khi đó, H là trung điểm của điểm M và M’).(1)
- Cách giải 2:
– Gọi M’ là điểm đối xứng của M(x;y) qua đường thẳng d: ax + by + c = 0 và H là trung điểm của đoạn MM’ (2)
– Từ (1) và (2), chúng ta tìm ra được tọa độ điểm M’
Tính chất 2 điểm đối xứng qua 1 điểm
Hai điểm được gọi là đối xứng với nhau qua một điểm nếu điểm đó là trung điểm của đoạn thẳng nối 2 điểm đó.
Tính chất của 2 điểm đối xứng qua 1 điểm là khoảng cách từ 2 điểm đến trung điểm bằng nhau và cùng nằm trên 1 đường thẳng.
Cách vẽ điểm đối xứng
Sử dụng định nghĩa của phép đối xứng trục.
- a) Hai điểm gọi là đối xứng vs nhau qua đường thẳng (d) nếu (d) là đường trung trực của đoạn thẳng nối 2 điểm đó.
Quy ước: Nếu B∈d thì điểm B đối xứng với B qua d.
- b) Hai hình được gọi là đối xứng với nhau qua đường thẳng (d) nếu mỗi điểm thuộc hình này đối xứng với điểm thuộc hình kia qua đường thẳng (d) và ngược lại. Đường thẳng d chính là trục đối xứng của 2 hình đó.
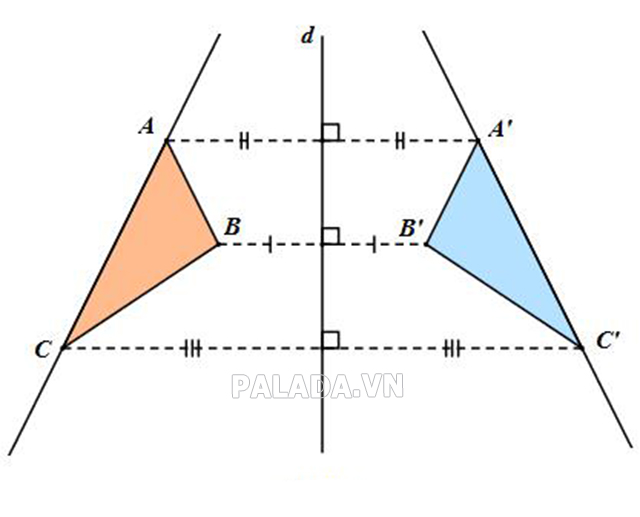
Sử dụng tính chất:
Nếu các điểm A và A’, B và B’, C và C’ đều đối xứng với nhau qua đường thẳng (d); trong đó C nằm giữa 2 điểm A và B thì C’ nằm giữa 2 điểm A’ và B’
Một số ví dụ về tìm điểm đối xứng
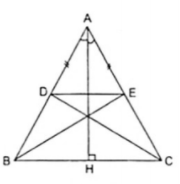
Ví dụ 1. Cho ΔABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, điểm E đối xứng với D qua đường cao AH.
Giải
Vì ABC cân tại A nên ta có AH là đường cao.
Theo giả thiết nên AH là tia phân giác góc A.
Vẽ điểm E thuộc cạnh AC cho AD = AE nên ∆ADE cân tại A => AH là đường trung trực của DE. Vậy điểm D đối xứng với E qua AH.
Ví dụ 2. Cho ΔABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D. Sau đó vẽ ΔADC đối xứng với ΔAEB qua AH.
Giải
Vì AH là đường cao của ΔABC cân ở A nên AH là đường trung trực của BC
=> B đối xứng với C qua AH.
Vẽ điểm E thuộc cạnh AC với AD = AE nên ΔADE cân tại A => AH là đường trung trực của DE. Vậy D đối xứng với điểm E qua AH.
Lại có, điểm A đối xứng với A qua AH theo quy ước. Vậy ΔADC đối xứng với ΔAEB qua đường cao AH.
Ví dụ 3. Cho tam giác ABC, trong đó AB = 11cm, AC = 16 cm. Vẽ hình đối xứng với ΔABC qua trục là cạnh BC.
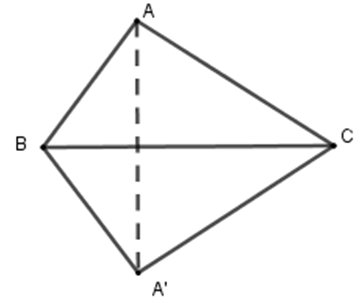
Giải
Ta có B đối xứng với điểm B qua BC theo quy ước, C đối xứng với điểm C qua BC theo quy ước
Vẽ đường thẳng (d) đi qua điểm A và vuông góc với BC. Trên đường thẳng (d), vẽ điểm A’ sao cho AB = A’B=> A’ là điểm đối xứng với A qua BC. Khi đó tam giác A’BC đối xứng với ΔABC qua BC.
Ví dụ 4. Cho hai điểm A, B nằm cùng phía với đường thẳng (d). Vẽ 2 điểm C đối xứng với điểm A qua (d) và điểm D đối xứng với điểm B qua (d).
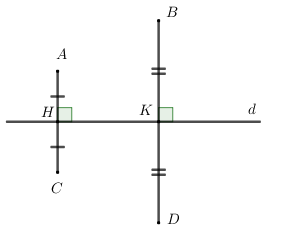
Giải
Vẽ 
. Vẽ hai điểm C, D sao cho H là trung điểm của đoạn AC, K là trung điểm của đoạn BD, ta được C đối xứng với điểm A qua đường thẳng (d), D đối xứng với B qua đường thẳng (d).
Tính chất đường trung trực của tam giác, định nghĩa và bài tập
Vậy là bài viết đã giải thích điểm đối xứng là gì, cách vẽ và cách tìm điểm đối xứng trong hình học. Vị trí điểm đối xứng có ý nghĩa quan trọng trong giải toán hình. Bởi vậy, các bạn cần chú ý tính chất của vị trí điểm đặc biệt này để vận dụng vào giải nhanh và chính xác bài tập.
