Hình chóp tam giác đều là một trong những hình học không gian mà chúng ta đã được làm quen từ năm cấp 2. Bài viết sau đây Palada.vn sẽ tổng kết về định nghĩa, tính chất, công thức tính chu vi, diện tích và thể tích hình chóp đều cùng các dạng bài tập liên quan. Bạn nào lỡ quên kiến thức về hình chóp tam giác đều thì tham khảo nhé.
Tóm tắt
- 1 Hình chóp là gì?
- 2 Hình chóp tam giác đều là gì?
- 3 Công thức tính chu vi hình chóp tam giác đều
- 4 Công thức tính diện tích hình chóp tam giác đều
- 5 Công thức tinh thể tích hình chóp tam giác đều
- 6 Cách vẽ hình chóp tam giác đều bằng 3 bước đơn giản
- 7 Phân biệt các hình chóp
- 8 Dạng toán thường gặp về hình chóp tam giác đều
Hình chóp là gì?
Định nghĩa hình chóp
- Hình chóp là hình học không gian, nó có mặt đáy là đa giác lồi và các mặt bên là tam giác có chung 1 đỉnh gọi là đỉnh của hình chóp
- Hình chóp có nhiều loại khác nhau, tên của hình chóp quy định theo hình mặt đáy. Hình chóp tam giác có mặt đáy là hình tam giác, hình chóp tứ giác có mặt đáy là hình tứ giác
- Trong các trường hợp mặt đáy là các hình đặc biệt như tam giác đều hay tứ giác đều thì đó gọi là hình chóp đều
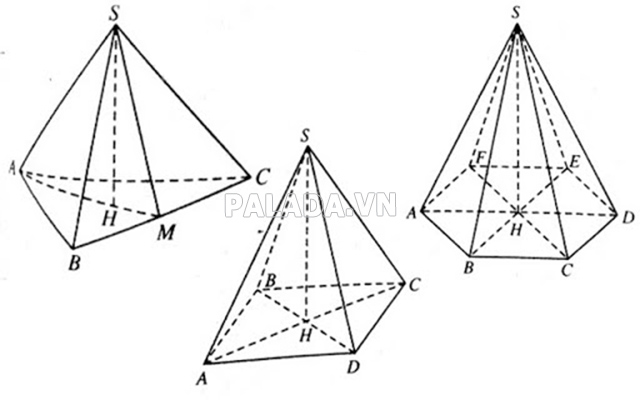
Tính chất hình chóp
- Đường cao của hình chóp là đường thẳng đi qua 1 đỉnh và vuông góc với mặt phẳng đáy của hình chóp đó
- Tên gọi của hình chóp dựa vào hình dạng mặt đáy của hình chóp đó
- Nếu hình chóp có cạnh bên tạo với mặt đáy các góc bằng nhau hoặc các cạnh bằng nhau thì chân đường cao vừa là tâm đường tròn ngoại tiếp đáy.
- Nếu hình chóp có các mặt bên tạo với mặt đáy góc bằng nhau hoặc có các đường cao của mặt bên xuất phát từ 1 đỉnh bằng nhau thì chân đường cao cũng chính là tâm đường tròn nội tiếp mặt đáy.
- Nếu hình chóp có mặt bên hoặc mặt chéo bất kỳ vuông góc với mặt đáy thì đường cao của hình chóp đồng thời cũng là đường cao của mặt bên hoặc mặt chéo đó.
Hình chóp tam giác đều là gì?
Định nghĩa hình chóp tam giác đều
Hình chóp tam giác đều là hình chóp có mặt đáy là tam giác đều, các mặt bên đều là tam giác cân bằng nhau có chung đỉnh
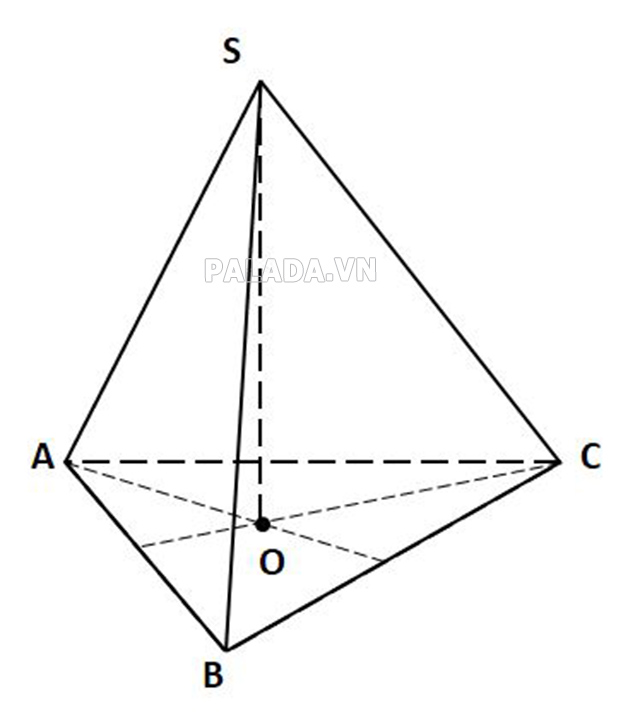
Tính chất hình chóp tam giác đều
- Hình chóp tam giác đều bất kỳ có 3 mặt phẳng đối xứng
- Hình chóp có mặt đáy là tam giác đều
- Các cạnh bên bằng nhau
- Tất cả các mặt bên đều là những hình tam giác cân và bằng nhau
- Chân đường cao trùng với tâm của mặt phẳng đáy (tâm mặt đáy là trọng tâm của tam giác)
- Số đo góc tạo bởi các mặt bên và mặt đáy bằng nhau
- Số đo góc tạo bởi cạnh bên và mặt đáy bằng nhau
***Lưu ý:
Tâm của tam giác đều là giao điểm của 3 đường trung tuyến, vừa là đường cao, đường trung trực và đường phân giác trong.
Công thức tính chu vi hình chóp tam giác đều
Chu vi hình chóp được tính bằng tổng chu vi mặt đáy và các mặt bên
Công thức
| P= Pđáy + Pcác mặt bên |
Trong đó
Pđáy là chu vi mặt đáy
Pcác mặt bên là chu vi các mặt bên
Công thức tính diện tích hình chóp tam giác đều
Diện tích hình chóp tam giác đều gồm có diện tích xung quanh và diện tích toàn phần.
- Diện tích xung quanh hình chóp tam giác đều
Diện tích xung quanh của hình chóp tam giác đều được tính bằng tích của nửa chu vi đáy với trung đoạn
Công thức
| Sxq = p.d |
Trong đó: p là nửa chu vi đáy
d là trung đoạn của hình chóp tam giác đều. Trung đoạn là đường cao xuất phát từ đỉnh dóng xuống trung điểm của 1 cạnh.
- Diện tích toàn phần hình chóp tam giác đều
Diện tích toàn phần của hình chóp tam giác đều được tính bằng tổng diện tích xung quanh và diện tích đáy
| Stp = Sxq + Sđáy |
Như vậy, muốn tính được diện tích xung quanh và diện tích toàn phần của hình chóp tam giác đều, bạn cần phải tính được độ dài trung đoạn và chu vi cùng diện tích mặt đáy.
Công thức tinh thể tích hình chóp tam giác đều
Tương tự như công thức tính thể tích hình chóp. Công thức tính thể tích hình chóp tam giác đều cụ thể như sau:
| V=1/3(S.h) |
Trong đó:
S là diện tích đáy
h là chiều cao
Cách vẽ hình chóp tam giác đều bằng 3 bước đơn giản
- Bước 1: Vẽ mặt đáy hình chóp là tam giác đều ABC (nhưng không nhất thiết phải vẽ 3 cạnh bằng nhau hoàn toàn mà có thể vẽ tam giác thường), AC vẽ nét đứt
Bước 2: Vẽ 2 đường trung tuyến CF và AI giao nhau tại điểm O, O chính là chân đường cao trùng với tâm đáy
Bước 3: Từ O, dựng đường thẳng đứng, ta được đỉnh S, từ S nối với đỉnh A, B, C
=> Hoàn thành cách dựng hình chóp tam giác đều SABC có: SO là đường cao, SA = SB = SC.
Phân biệt các hình chóp
| Hình chóp tam giác đều | Hình chóp tứ giác đều | Hình chóp ngũ giác đều | Hình chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác đều | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |
Dạng toán thường gặp về hình chóp tam giác đều
Xác định mối quan hệ giữa các yếu tố cạnh và mặt phẳng của hình chóp tam giác đều
+ Sử dụng mối quan hệ vuông góc và song song giữa các đường thẳng và mặt phẳng.
+ Sử dụng các kiến thức tổng hợp về hình chóp tam giác đều
Bài tập vận dụng
Cho hình chóp tam giác đều SABC cạnh đáy bằng a, mặt bên tạo với đáy một góc 60 độ. Tính thể tích khối chóp SABC.
Hướng dẫn:
– Dựng khối chóp tam giác đều SABC.
– Gọi điểm I là tâm đáy => SI vuông góc với mặt phẳng đáy ABC.
=> VSABC = 1/3. SI. Stam giác ABC
– Tính: SABC = a2√3 : 4
– Tính SI:
+ Góc tạo bởi mặt bên (SBC) và mặt đáy (ABC) = góc SDI = 60 độ
Ta có: ID = 1/3. AD = 1/3. (a√3 : 2) = b : 2√3 (tính chất đường cao, đường trung tuyến AD của tam giác đều)
+ Xét tam giác vuông SID có: tanSDI = đối/kề = SI : ID
=> SI = (a : 2√3) . √3
=> SI = a/2
=> VSABC = 1/3 . a/2. a2√3 : 4 = a3√3/24 (đvtt).
Hình hộp chữ nhật là gì? Công thức tính diện tích hình hộp chữ nhật
Hình vuông là gì? Công thức tính chu vi hình vuông, diện tích
Hy vọng với những tổng hợp kiến thức lý thuyết cùng bài tập vận dụng trên đây đã giúp bạn hiểu được hình chóp tam giác đều là hình như thế nào, có những tính chất gì, công thức tính chu vi, diện tích và thể tích hình chóp tam giác đều ra sao. Hãy tích cực luyện giải các bài toán về hình chóp tam giác đều liên quan để thuần thục cách giải cũng như rèn khả năng ghi nhớ kiến thức nhé!
