Kiến thức về 2 tam giác đồng dạng lớp 8 chúng ta đã được tìm hiểu. Cách chứng minh tam giác đồng dạng được đưa vào giảng dạy trong chương trình Toán lớp 9. Ở bài viết sau, Palada.vn sẽ giúp các bạn học sinh hệ thống lại kiến thức về 2 tam giác đồng dạng cùng các bài tập chứng minh 2 tam giác đồng dạng, cùng tham khảo nhé!
Tóm tắt
2 tam giác đồng dạng là gì?
Khái niệm hai tam giác đồng dạng
2 tam giác đồng dạng khi nào? Hai tam giác đồng dạng khi chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ nhau.
*Các TH đồng dạng của tam giác thường
Tam giác đồng dạng là:
- Hai tam giác có 3 cặp cạnh tương ứng tỉ lệ vs nhau là tam giác đồng dạng (cạnh-cạnh-cạnh).
Ví dụ minh họa:
Xét △ABC và △A’B’C’, ta có:
=
=
⇾△ABC ~ △A’B’C’ (C-C-C)
- Hai tam giác có 2 cặp góc tương ứng bằng nhau là tam giác đồng dạng. (góc-góc).
Ví dụ minh họa:
Xét △ABC và △A’B’C’, ta có:
=⇾
=
⇾△ABC ~ △A’B’C’ (C-G-C)
- Hai tam giác có 2 cặp cạnh tương ứng tỷ lệ + góc xen giữa 2 cặp cạnh ấy bằng nhau là tam giác đồng dạng. (cạnh-góc-cạnh).
Ví dụ minh họa:
Xét △ABC và △A’B’C’, ta có:
=; 
=
⇾△ABC ~ △A’B’C’ (G-G)
*Các TH đồng dạng tam giác vuông
Định lí 1 Nếu cạnh huyền + cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền + cạnh góc vuông của tam giác kia thì 2 tam giác đó đồng dạng.
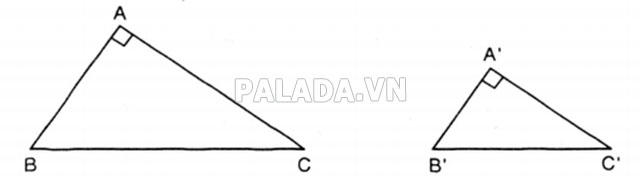
Ví dụ minh họa:
Giả thiết: △ABC và △A’B’C’, ==90०; 
=
Kết luận: ⇾△ABC ~ △A’B’C’
Định lí 2 : Nếu 2 cạnh góc vuông của tam giác vuông này tỉ lệ với 2 cạnh góc vuông của tam giác vuông kia thì 2 tam giác đó đồng dạng. (hai cạnh góc vuông)
Ví dụ minh họa:
Giả thiết: △ABC và △A’B’C’, ==90०; =
Kết luận: ⇾△ABC ~ △A’B’C’
Định lí 3: Nếu góc nhọn của tam giác vuông này = góc nhọn của tam giác vuông kia thì 2 tam giác đó cũng đồng dạng. (góc)
Giả thiết: △ABC và △A’B’C’, ==90०
=⇾△ABC ~ △A’B’C’
Tính chất tam giác đồng dạng là gì?
Từ 2 tam giác đồng dạng, chúng ta suy ra được:
- Tỉ số 2 đường phân giác, đường cao, đường trung tuyến, bán kính nội tiếp và ngoại tiếp, chu vi tương ứng của hai tam giác đồng dạng đó bằng với tỉ số đồng dạng.
- Tỉ số diện tích của 2 tam giác đồng dạng = bình phương tỉ số đồng dạng.
Cách chứng minh 2 tam giác đồng dạng
Chứng minh hai tam giác đồng dạng – Hệ thức
Bài toán: Cho △ABC(AB<AC), AD là phân giác. Miền ngoài vẽ tia Cx cho 
= 
. Gọi I là giao điểm của Cx, AD. Chứng minh rằng:
- a) △ADB∼△CDI
- b) AD.AC=AB.AI
c)AD2 = AB.AC – BD.DC
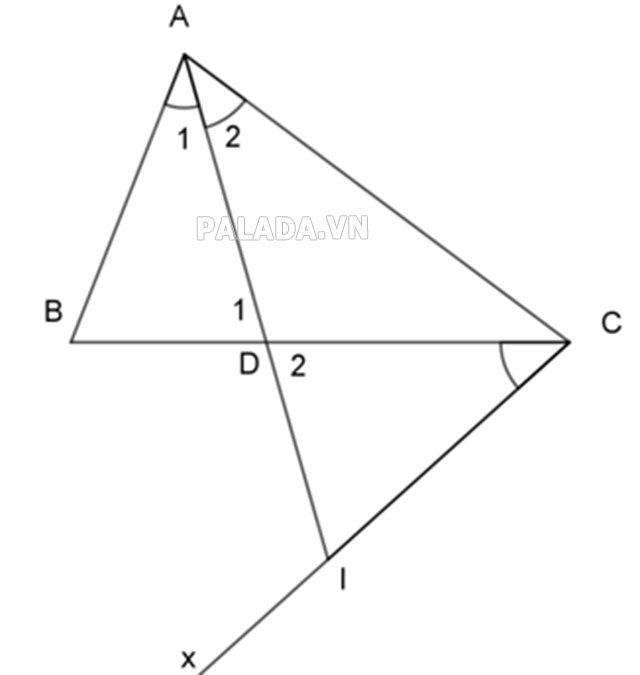
- ∆ADB và ∆CDI , ta có 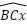= 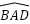: (gt)
⇾
= 
(đối đỉnh) => ∆ADB ~ ∆CDI
- b) ∆ABD và ∆AIC , ta có : =
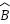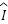(∆ADB ~ ∆CDI); 
= 
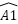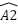(AD là phân giác)
=> ∆ABD ~ ∆AIC =>
=
⇾AD.AI = AB.AC (1)
- c) Có
=
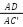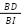; (∆ADB ~ ∆CDI ) => AD.DI = BD.CD (2) từ (1) và (2) : AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
-Chứng minh hai tam giác đồng dạng – Định lí Talet + 2 đường thẳng song song
Bài toán: Cho ∆ABC nhọn, đường cao BD; CE. Kẻ 2 đường cao DF; EG của ∆ADE. Chứng minh:
- a) △ADB∼△AEG
- b) AD.AE = AB.AG = AC.AF
- c) FG // BC
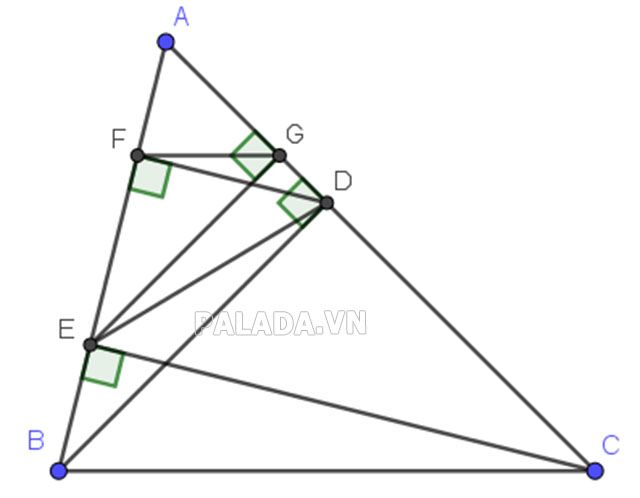
- a) Xét ∆ABD và ∆AEG, ta có :
BD⊥AC (BD là đường cao)
EG⊥AC (EG là đường cao)
Suy ra: BD // EG
Suy ra: △ADB∼△AEG
- b) Từ a) Suy ra được ABAE=ADAG
⇒ AD.AE = AB.AG (1)
CM tương tự, ta được : AD.AE = AC.AF (2)
Từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
- c) Xét tam giác ABC, ta có :
AB.AG = AC.AF (cmb) suy ra: 
=
Suy ra: FG // BC (Talet đảo)
-Chứng minh 2 tam giác đồng dạng – góc tương ứng bằng nhau
Bài toán: Cho △ABC có 2 đường cao BD + CE cắt nhau tại H. Chứng minh:
- a) △HBE∼△HCE
- b) △HED∼△HBC
và 
= 
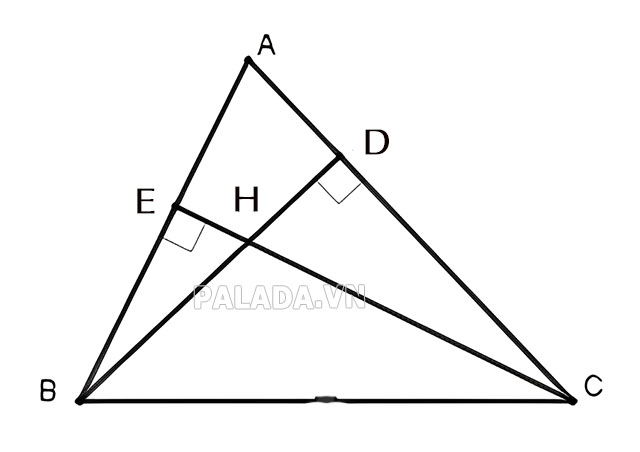
- a) Xét △HBE và △HCD, ta có :
= 
=90∘ (gt)
= 
(đối đỉnh)
Suy ra: △HBE∼△HCD (g – g)
- b) Xét △HED và △HBC, ta có :
=
(△HBE∼△HCD)
Suy ra: =
= (đối đỉnh)
Suy ra △HED∼△HBC(c – g – c)
Suy ra: = 
(1)
Lại có: đường cao BD + CE cắt nhau tại H (gt)
Do đó, điểm H là trực tâm => AH⊥BC tại M.
Suy ra = 
=90∘
Mặt khác : = =90∘
Suy ra: = (2)
Từ (1) và (2) => =
hay: =
Tổng hợp các cách chứng minh 2 tam giác đồng dạng lớp 8
- Phương pháp 1: Hai tam giác đồng dạng khi mà chúng có các cặp cạnh tương ứng tỉ lệ + các góc tương ứng tỉ lệ.
- Phương pháp 2: Định lý Talet: Đường thẳng song song vs 1 cạnh của tam giác + cắt 2 cạnh còn lại sẽ vạch ra trên cạnh đó những đoạn thẳng tương ứng tỷ lệ.
- Phương pháp 3: CM các điều kiện cần và đủ để 2 tam giác đồng dạng: 2 tam giác có các cặp cạnh tương ứng tỷ lệ sẽ đồng dạng; 2 tam giác có 2 cặp góc tương ứng bằng nhau sẽ đồng dạng; 2 tam giác có 2 cặp cạnh tương ứng tỉ lệ, 2 góc xen giữa 2 cặp cạnh này bằng nhau sẽ đồng dạng.
- Phương pháp 4: Chứng minh TH 1 (cạnh-cạnh-cạnh): Nếu 3 cạnh của tam giác này tương ứng tỉ lệ với 3 cạnh của tam giác kia thì 2 tam giác đó sẽ đồng dạng.
- Phương pháp 5: Chứng minh TH 2 (cạnh-góc-cạnh): Nếu 2 cạnh của tam giác này tương ứng tỷ lệ với 2 cạnh của tam giác kia + 2 góc tạo bởi tạo các cặp cạnh đó bằng nhau thì 2 tam giác đó cũng đồng dạng.
Bài tập chứng minh tam giác đồng dạng toán 9 (có đáp án)
Dạng 1: Phương pháp CM 2 tam giác đồng dạng – Sử dụng hệ thức:
Bài tập: Cho tam giác ABC có góc A vuông, đường cao AH. CM các hệ thức sau:
- CMR AB2 = BH.BC và AC2 = CH.BC
- CMR AB2 +AC2 = BC2
- CMR AH2 = BH.CH
- CMR AH.BC = AB.AC
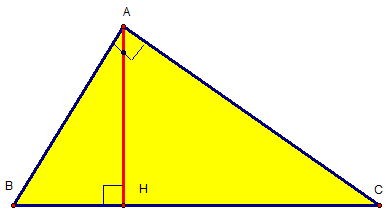
a.Xét tam giác ∆ABC và ∆ HAC, ta có:
Góc BAC = góc AHC = 90 độ
Góc C là góc chung
=> Vậy tam giác ∆ABC ~ ∆HAC (theo định lý g – g trong tam giác vuông)
Vậy AC/HC = BC/AC
=> AC2 = CH.BC (1)
CM tương tự ta có : AB2 = BH.BC (2)
- Từ (1) và (2) vừa chứng minh ở trên, ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
- Xét 2 tam giác ∆HBA và ∆HAC, ta có :
Góc BHC = góc AHC = 90 độ
Góc ABH = CAH (cùng phụ góc BAH)
=> Vậy kết luận ∆HBA ~ ∆HAC (tính chất g – g trong tam giác vuông)
=> HA/HC = HB/HA
Vậy: AH2 = BH.CH
- Ta có ∆ABC ~ ∆HAC
=> HA/AB = AC/BC
Vậy: HA.BC = AB.AC
Dạng 2: Chứng minh hai tam giác đồng dạng – Định lí Talet + hai đường thẳng song song
Bài toán: Cho ∆ABC nhọn. Vẽ 2 đường cao là BD+CE. Lần lượt vẽ các đường cao DF+EG của ∆ADE. Yêu cầu:
- a) Hãy CMR ∆ABD ~ ∆AEG.
- b) Hãy CMR AD.AE = AB.AG = AC.AF
- c) Hãy CMR FG // BC
a) Xét ∆ABD và ∆AEG, ta có :
BD⊥AC (BD là đường cao)
EG⊥AC (EG là đường cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
- b) Ta có AB/AE = AD/AG
=> AD.AE = AB.AG (1)
Chứng minh tương tự : AD.AE = AC.AF (2)
Từ dữ kiện (1) và (2) suy ra : AD.AE = AB.AG = AC.AF
- c) Xét ∆ABC, ta có :
AB.AG = AC.AF => FG // BC (theo định lí đảo talet)
Dạng 3 : Phương pháp CM hai tam giác đồng dạng – các góc tương ứng bằng nhau
Bài toán: Cho ∆ABC có đường cao BD + CE cắt nhau tại H. Yêu cầu:
- a) CMR ∆HBE ~ ∆HCE.
- b) CMR ∆HED ~ ∆HBC và góc HDE = góc HAE
- c) Biết BD = CD. Gọi M là giao điểm của AH + BC. CMR DE vuông góc EM.
- a) Xét 2 ∆HBE và ∆HCD ta có :
Góc BEH = góc CDG = 90 độ (GT)
Góc H1 = góc H2 (đối đỉnh)
Suy có ∆HBE ~ ∆HCD (tính chất g – g)
- b) ∆HED và ∆HBC, ta có :
HE/HD = HB/HC (∆HBE ~ ∆HCD)
=> HE/HB = HD/HC
Mà góc EHD = góc CHB (đối đỉnh)
=> ∆HED ~ ∆HBC (do tính chất c – g – c)
=> Góc D1 = góc C1 (1)
mà : Đường cao BD+CE cắt nhau tại H (GT)
=> Điểm H là điểm trực tâm. => AH ~ BC tại M.
=> góc A1 + góc ABC = 90 độ
mặt khác: góc C1 + góc ABC = 90 độ (2)
=> Từ dữ kiện (1) và (2) có: góc A1 = D1
hay góc HDE = góc HAE
- c) CM tương tự câu b, ta có: góc A2 = E2 (3)
xét ∆BCD, ta có : DB = DC (GT)
=> ∆BCDcân tại D => góc B1 = góc ACB
mà góc B1 = góc E1 (vì ∆HED ~ ∆HBC)
=> Góc E1 = góc ACB
mà: góc A2 + góc ACB = 90 độ
Góc A2 = góc E2 (CMT)
=> Góc E1 + E2 = 90 độ
hay góc DEM = 90 độ
=> ED ~ EM.
Tính chất đường trung trực của tam giác, định nghĩa và bài tập
Hy vọng rằng với nội dung lý thuyết kết hợp các bài tập chứng minh tam giác đồng dạng trên đây đã giúp các bạn học sinh hiểu và ghi nhớ được 2 tam giác đồng dạng là gì. Đây là phần kiến thức nền quan trọng nên các bạn hãy chú ý giải thật nhiều bài tập liên quan để thuần thục, tránh sai sót để mất điểm không đáng có nhé!
