1001 bài toán khó nhất thế giới không chỉ đòi hỏi kiến thức sâu rộng mà còn yêu cầu một trí tuệ vượt trội, một tư duy sắc bén và khả năng giải quyết vấn đề tinh tế. Trong bài viết này, chúng ta sẽ khám phá những bài toán khó nhất thế giới vô cùng hại não mà chỉ những người có IQ cao mới có thể vượt qua.
Tóm tắt
Tổng hợp những bài toán khó nhất thế giới
Để nói rằng bài toán nào khó nhất thế giới thì thật khó có câu trả lời. Sau đây sẽ là 5 bài toán khó nhất trên thế giới hại não, có đáp án do Palada.vn tổng hợp.
1. Bài toán 281 năm chưa tìm ra lời giải của Christian Goldbach
Trong lĩnh vực Toán học, bài toán liên quan đến các số nguyên tố đã trở thành một trong những bài toán khó nhất thế kỷ. Một ví dụ điển hình là giả thuyết Goldbach, mà nhà toán học Christian Goldbach đã đề xuất cách đây 281 năm, và cho đến nay vẫn là bài toán khó nhất thế giới chưa giải được.
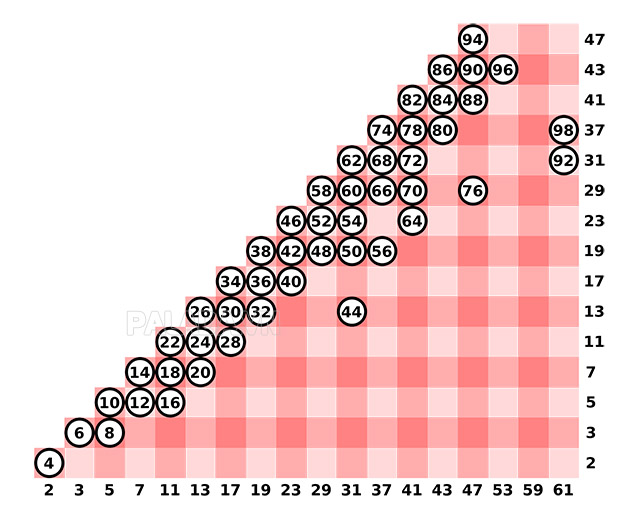
Vào năm 1742, trong một lá thư gửi tới một đồng nghiệp ở Thụy Sĩ, Goldbach đã đề cập đến vấn đề này như sau: “Mọi số nguyên lớn hơn 2 đều có thể được biểu diễn dưới dạng tổng của 3 số nguyên tố.” Ví dụ, 35 = 19 + 13 + 3 hoặc 77 = 53 + 13 + 11.
Trong suốt gần 300 năm qua, giả thuyết này đã được gọi là giả thuyết Goldbach tam nguyên và đã được nhiều nhà toán học nghiên cứu, nhưng cho đến nay, vẫn chưa có ai tìm ra được một lời giải.
Nhà toán học Terence Tao từ Đại học California, Los Angeles, Mỹ, đã tiến gần hơn đến việc giải quyết bài toán này. Ông đã chứng minh rằng mỗi số lẻ có thể được biểu diễn dưới dạng tổng tối đa 5 số nguyên tố. Hi vọng rằng trong tương lai không xa, chúng ta có thể giảm số lượng số nguyên tố cần để biểu diễn các số lẻ xuống còn 3 và hoàn toàn chứng minh giả thuyết Goldbach.
2. Bài toán “Ai giữ cá” của Einstein
Câu đố logic nổi tiếng của nhà bác học Albert Einstein từ thế kỷ 19 cũng là một trong các bài toán khó nhất thế giới đối với nhiều người. Theo Einstein, chỉ có 2% dân số thế giới có thể giải đáp câu đố này. Bài toán bao gồm 3 phần: các dữ kiện, một câu hỏi đơn giản và các “manh mối” để tìm lời giải.

Đề bài cho như sau:
Trong một khu phố, có 5 ngôi nhà có màu sắc khác nhau. Mỗi ngôi nhà thuộc về một chủ sở hữu có quốc tịch khác nhau. Mỗi người lại có sở thích đồ uống riêng, hút một nhãn hiệu thuốc lá khác nhau và nuôi một con vật cưng riêng. Không có hai người nào có cùng loại vật nuôi, hút cùng một nhãn hiệu thuốc lá hoặc thích cùng một loại đồ uống.
Gợi ý:
- Người Anh đang sống trong ngôi nhà màu Đỏ.
- Người Thuỵ Điển nuôi một chú Chó.
- Người Đan Mạch rất thích uống Trà.
- Ngôi nhà màu Xanh Lá bên trái ngôi nhà màu Trắng.
- Chủ nhà ngôi nhà Xanh Lá rất thích uống Cà Phê.
- Người hút thuốc lá Pall Mall đang nuôi Chim.
- Chủ nhà màu Vàng có sở thích hút thuốc lá Dunhill.
- Người sống trong ngôi nhà ở chính giữa phố thích uống Sữa.
- Người Na Uy đang sống trong ngôi nhà đầu tiên.
- Người hút thuốc lá Blends sống bên cạnh người nuôi Mèo.
- Người nuôi Ngựa sống bên cạnh người hút thuốc lá Dunhill.
- Người hút thuốc Blue Master thì thích uống Bia.
- Người Đức hút thuốc lá hiệu Prince.
- Người Na Uy sống bên cạnh ngôi nhà màu Xanh Lơ.
- Người hút thuốc lá Blends có người hàng xóm rất thích Nước khoáng.
Vậy ai sẽ là người nuôi cá?
Từ câu hỏi trên, bạn thấy mình nằm trong số 2% người thông minh nhất thế giới hay sẽ thuộc nhóm 98% còn lại? Đáp án người nuôi cá là người Đức.
3. Bài toán siêu hóc búa chỉ 0,001% người trong cuộc thi giải được
Bài toán này được xem là một trong những bài toán khó nhất trên thế giới. Nó đã xuất hiện trong kỳ thi SAT năm 1982, chỉ có 3 trong số 300.000 thí sinh đã đưa ra câu trả lời chính xác.
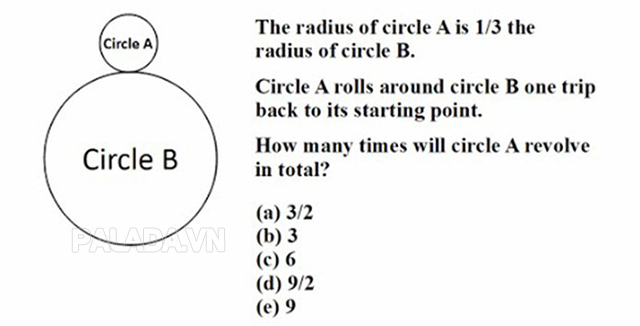
Đề bài: Bán kính của hình tròn B to gấp 3 lần bán kính của hình tròn A. Nếu hình tròn A lăn quanh hình tròn B, thì cần bao nhiêu vòng quay để trở lại điểm xuất phát?
Các lựa chọn đưa ra là: 3/2 vòng, 3 vòng, 6 vòng, 9/2 vòng, 9 vòng.
Rất nhiều người và hầu hết các thí sinh tham gia kỳ thi SAT đã chọn lựa chọn số 3 là đáp án đúng.
Nếu ta coi hệ quy chiếu là hình tròn A, thì nó chỉ cần quay quanh 3 vòng. Tuy nhiên, nếu ta không coi hệ quy chiếu trên hình tròn A, mà coi hệ quy chiếu trên một điểm bất kỳ không nằm trên hình tròn A, thì nó đã quay được 4 vòng. Vòng thứ tư là do hình tròn B tặng thêm khi A lăn quanh B.
4. Bài toán tìm sinh nhật Cheryl
Albert và Bernard mới kết bạn với Cheryl và muốn biết ngày sinh nhật của cô ấy. Cheryl đưa ra 10 ngày có khả năng là sinh nhật mình: Ngày 15/5, 16/5, 19/5, 17/6, 18/6, 14/7, 16/7, 14/8, 15/8 và 17/8. Cheryl sau đó cũng đã tiết lộ tháng và ngày sinh cho Albert và Bernard riêng tư.

Albert nói: “Tôi không biết ngày sinh của Cheryl, nhưng tôi biết Bernard cũng không biết”.
Bernard nói: “Ban đầu tôi cũng không biết ngày sinh của Cheryl, nhưng bây giờ tôi biết rồi”.
Albert nói: “Vậy tôi cũng biết ngày sinh nhật của Cheryl”.
Theo bạn, ngày sinh nhật của Cheryl rơi vào ngày nào? Đây là một câu hỏi trong cuộc thi Olympic Toán học của châu Á năm 2015. Thực tế, mục đích của câu hỏi là kiểm tra khả năng suy luận của thí sinh, chứ không phải kỹ năng toán học của họ.
Lời giải bài toán sinh nhật Cheryl như sau:
Cheryl đưa ra cho Albert và Bernard một danh sách gồm 10 ngày có thể là ngày sinh nhật của cô ấy: ngày 15, 16, 19 tháng 5, ngày 17, 18 tháng 6, ngày 14, 16, 19 tháng 7 và ngày 14 tháng 8.
Thông qua một loạt các lời thoại, chúng ta có thể suy luận các thông tin sau:
– Cheryl cho biết Bernard không biết ngày sinh nhật của cô.
– Albert biết Bernard không biết, tức là Albert biết ngày sinh nhật của Cheryl.
– Albert biết ngày sinh nhật của Cheryl sau khi nghe câu nói đầu tiên của Cheryl.
Dựa vào những thông tin này, chúng ta có thể suy ra được ngày sinh nhật của Cheryl.
Chúng ta loại bỏ ngay hai ngày 18 và 19 do chỉ xuất hiện một lần trong danh sách của Cheryl. Điều này có nghĩa là Bernard không thể biết ngày sinh nhật của Cheryl từ danh sách ban đầu.
Tiếp theo, chúng ta xem xét câu nói của Albert. Nếu Cheryl nói với Albert rằng sinh nhật của cô ấy là tháng 5 hoặc tháng 6, thì Bernard có thể biết đáp án. Tuy nhiên, Albert khẳng định Bernard không biết, vì vậy Cheryl không thể có sinh nhật vào tháng 5 hoặc tháng 6.
Vì Albert biết ngày sinh nhật của Cheryl sau câu nói đầu tiên của cô, ta có thể suy ra rằng câu nói đầu tiên của Cheryl không chứa ngày 18 hoặc 19, vì nếu có, Albert sẽ không biết ngày sinh nhật của Cheryl ngay sau đó.
Sau khi loại bỏ ngày 18 và 19, ta còn lại 8 ngày: ngày 15, 16, 17 tháng 7 và ngày 14, 16 tháng 8. Cheryl nói với Bernard rằng Bernard không biết ngày sinh nhật của cô.
Nếu Cheryl nói với Bernard rằng sinh nhật của cô là ngày 14, Bernard sẽ không thể biết ngày sinh nhật của cô, vì có hai ngày 14 trong danh sách. Vậy ta loại bỏ ngày 14, chỉ còn lại 3 ngày: ngày 15, 16 tháng 7 và ngày 16 tháng 8.
Sau câu nói của Bernard, Albert cũng biết ngày sinh nhật của Cheryl. Nếu Cheryl nói với Albert rằng sinh nhật của cô là trong tháng 8, Albert cũng không thể biết đáp án.
Vậy ngày sinh nhật của Cheryl là ngày 16 tháng 7 (July 16).
5. Bài toán về hiệp sĩ – kẻ nói dối
Bài toán khó nhất thế giới này rất được ưa thích ở Nga và đã xuất hiện trong kỳ thi Olympic cho học sinh lớp 9.

Đề bài: 30 người ngồi quanh một bàn tròn có 30 chiếc ghế, được đánh số từ 1 đến 30. Trong số đó, một số là hiệp sĩ và một số là kẻ lừa dối. Hiệp sĩ luôn nói sự thật, trong khi kẻ lừa dối luôn nói dối.
Mỗi người có chính xác một người bạn trong nhóm. Bạn của hiệp sĩ là kẻ lừa dối và ngược lại. Mỗi người được hỏi: “Có phải bạn của bạn đang ngồi bên cạnh bạn không?” 15 người đang ngồi ở vị trí lẻ đều trả lời: “Đúng”. Tìm số người đang ngồi ở vị trí chẵn cũng trả lời: “Đúng.”
Lời giải: Từ đề bài, ta suy ra rằng trong số 30 người, có 15 cặp bạn hiệp sĩ và kẻ lừa dối. Ta có thể dễ dàng đoán đáp án bằng cách giả định rằng tất cả 15 người ngồi ở vị trí lẻ đều là hiệp sĩ. Trong trường hợp này, bạn của họ sẽ ngồi ở các vị trí chẵn và đều là kẻ lừa dối, do đó không ai sẽ trả lời “Đúng”. Vậy đáp án là 0.
Tuy nhiên, đó chỉ là một dự đoán chứ không phải lời giải. Để chứng minh điều này, ta cần cung cấp một lời giải chứ không chỉ đưa ra một ví dụ như vậy.
Nếu chúng ta cố gắng xét tất cả các vị trí ngồi của 30 người, sẽ rất phức tạp vì có nhiều trường hợp khác nhau. Tuy nhiên, một nhận xét quan trọng là: Trong mỗi cặp bạn, chỉ có một người sẽ trả lời “Đúng” khi được hỏi “Có phải bạn của bạn đang ngồi bên cạnh bạn không?” Điều này có nghĩa là nếu có hai người, một hiệp sĩ và một kẻ lừa dối là bạn của nhau, xét hai trường hợp:
– Nếu họ ngồi bên cạnh nhau, thì hiệp sĩ sẽ trả lời “Đúng”, trong khi kẻ lừa dối sẽ trả lời “Không”.
– Nếu họ không ngồi bên cạnh nhau, thì hiệp sĩ sẽ trả lời “Không”, trong khi kẻ lừa dối sẽ trả lời “Đúng”.
Vì có 15 cặp bạn, ta có chính xác 15 câu trả lời “Đúng”. Vì tất cả 15 người ở vị trí lẻ đã trả lời “Đúng”, nên tất cả những người ở vị trí chẵn đều sẽ trả lời “Không”. Tức là đáp án là 0.
Trên đây là tổng hợp những bài toán khó nhất thế giới cùng lời giải. Chúng không chỉ là những câu đố thú vị mà còn là cơ hội để chúng ta nâng cao khả năng tư duy và rèn luyện trí tuệ của mình. Dù bạn có IQ cao hay không, hãy luôn đối mặt với những thử thách này với sự tò mò, sẵn sàng học hỏi để khám phá bản thân và mở rộng ranh giới của trí tuệ con người.



