Số chính phương là gì chúng ta đều đã được tìm hiểu trong chương trình toán lớp 7. Bạn còn nhớ số chính phương là số như thế nào không? Nếu lỡ quên thì Palada.vn sẽ tổng kết lại nội dung cơ bản nhất về số chính phương qua bài viết sau nhé.
Tóm tắt
Định nghĩa về số chính phương là gì?
Số chính phương chính bằng bình phương của 1 số nguyên. Hiểu đơn giản, số chính phương là một số tự nhiên sẽ có căn bậc 2 cũng là một số tự nhiên.
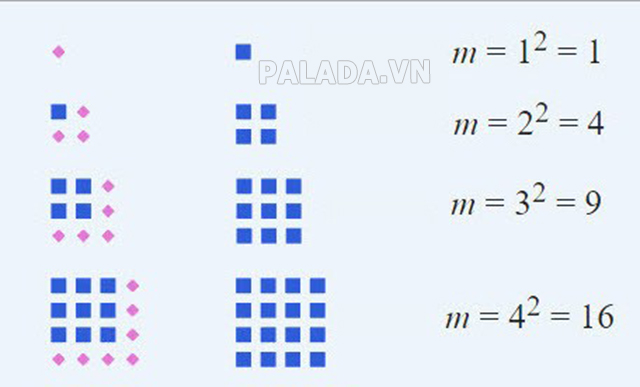
Số tự nhiên chính phương về bản chất là bình phương của 1 số tự nhiên nào đó. Hiểu theo một cách khác thì số chính phương thể hiện diện tích 1 hình vuông với chiều dài là cạnh số nguyên kia.
Với số nguyên gồm các số nguyên dương (1, 2, 3,…), số nguyên âm (-1, -2, -3,…) và số 0.
Các dạng số chính phương
Có 2 dạng số chính phương là:
| Số chính phương chẵn | Số chính phương lẻ |
| Số chính phương chẵn khi nó là bình phương của một số nguyên chẵn. | Số chính phương lẻ khi nó là bình phương của một số nguyên lẻ. |
| Ví dụ: Số 64 là một số chính phương chẵn vì nó là bình phương của số 8 (số chẵn). | Ví dụ: Số 25 là một số chính phương lẻ vì nó là bình phương của số 5 (số lẻ). |
Ví dụ số chính phương
Các số 4, 9, 16, 25, 36, 49, 64, 144, 225, 576 đều là số chính phương.
4= 22 là ví dụ cho một số chính phương chẵn
9= 32 là ví dụ cho một số chính phương lẻ
16= 42 là ví dụ cho một số chính phương chẵn
25 = 52 là ví dụ cho một số chính phương lẻ
36= 62 là ví dụ cho một số chính phương chẵn
225 = 152 là ví dụ cho một số chính phương lẻ
289 = 172 là ví dụ cho một số chính phương lẻ
576 = 242 là ví dụ cho một số chính phương chẵn
Dấu hiệu nhận biết số chính phương
Từ định nghĩa về số chính phương thì bạn cần phải nắm được dấu hiệu nhận biết số chính phương như sau:
- Số tận cùng (hàng đơn vị): Số chính phương chỉ có tận cùng (hàng đơn vị) là 0, 1, 4, 5, 6, 9. Ngược lại thì các số tận cùng là 2, 3, 7, 8 chắc chắn không phải là số chính phương.
- Dựa vào các tính chất cơ bản của số chính phương.
Tính chất của số chính phương là gì?
- Số chính phương chỉ có thể kết thúc bằng 0, 1, 4, 5, 6, 9; không thể kết thúc ở số tận cùng bằng 2, 3, 7, 8.
- Khi phân tích ra thừa số nguyên tố, số chính phương chứa các thừa số nguyên tố có số mũ chẵn.
- Số chính phương chỉ có thể có 1 trong 2 dạng là 4n hoặc 4n + 1. Không có số chính phương nào biểu diễn dạng là 4n + 2 hay 4n + 3 (n∈N).
- Số chính phương chỉ có thể có 1 trong 2 dạng là 3n hoặc 3n + 1. Không có số chính phương nào biểu diễn dạng 3n + 2 (n∈N).
- Số chính phương có chữ số tận cùng bằng 1 hoặc 9 thì chữ số hàng chục sẽ là chữ số chẵn.
- Số chính phương tận cùng là 5 thì chữ số hàng chục sẽ bằng 2.
- Số chính phương có tận cùng là 4 thì số hàng chục là số chẵn.
- Số chính phương tận cùng là 6 thì chữ số hàng chục là số ẻ.
- Số chính phương chia hết cho 2 thì chắc chắn chia hết cho 4.
- Số chính phương chia hết cho 3 thì chắc chắn chia hết cho 9.
- Số chính phương chia hết cho 5 thì chắc chắn cũng chia hết cho 25.
- Số chính phương chia hết cho 8 thì chắc chắn chia hết cho 16.
Cách tìm số chính phương
Thuật toán tìm số chính phương là một trong những thuật toán căn bản khi bạn mới bắt đầu học lập trình. Nó giúp người học rèn luyện được tính tư duy logic của bản thân. Để xác định được một số có phải là số chính phương hay không. Chúng ta thường sử dụng 2 cách dưới đây:
– Kiểm tra số chính phương bằng phương pháp vòng lặp. Sử dụng hàm kiểm tra số chính phương sqrt() trong math.h. Đây chính là phương pháp tìm số chính phương tối ưu hơn cả.
Cách 1: Sử dụng vòng lặp
Lặp i chạy từ 0 đến khi i*i > n. Nếu i * i = n thì n chính là số chính phương, sau đó kết thúc chương trình.
Nếu i * i > n thì n sẽ không phải là số chính phương.
Cách 2: Kiểm tra bằng hàm
Thao tác kiểm tra này sẽ đơn giản hơn rất nhiều so với cách sử dụng vòng lặp ở trên. Trong thư viện math.h có 1 hàm được sử dùng để tính căn bậc hai, đó chính là hàm sqrt().
Chúng ta sẽ sử dụng hàm sqrt() để đặt điều kiện cho n. Nếu sqrt(n) * sqrt(n) = n, thì n là số chính phương và ngược lại.
Kiểm tra số chính phương Pascal: Ngoài cách dùng hàm và vòng lặp đã đề cập ở trên, ta có thể sử dụng cách viết chương trình kiểm tra số chính phương bằng Pascal.
Các dạng toán tìm số chính phương
Dạng 1: Dạng nhận biết
Để giải quyết những dạng bài tập này, bạn cần phải nắm chắc khái niệm số chính phương là gì cùng các tính chất đặc trưng của số chính phương.
VD: Cho dãy số sau, xác định số nào là số chính phương 9, 81, 790, 400, 121, 380, 2500, 441, 560.
Trả lời: Trong dãy số trên, các số chính phương là: 9 = 3²; 81 = 9²; 121 = 11²; 400 = 20²; 441 = 21²
Dạng số 2: Chứng minh một số là số chính phương hoặc không phải là số chính phương
Riêng đối với dạng bài tập chứng minh số chính phương thì các bạn không chỉ cần nắm vững kiến thức về số chính phương mà cần có tư duy logic, nhanh nhạy khi làm.
Ví dụ 1: Hãy chứng minh số 1237562890 không phải là số chính phương.
Lời giải:
Ta nhận thấy, số 1237562890 có tận cùng bằng 0 nên chia hết cho 5, nhưng lại không chia hết cho 25.
Theo tính chất của số chính phương => số 1237562890 không phải là số chính phương
Ví dụ 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 số bất kì luôn là số chính phương.
Lời giải:
Giả sử, 4 số tự nhiên liên tiếp có dạng: n, n+1, n+2, n+3 với n € số tự nhiên.
Khi đó, ta có:
A = n(n+1)(n+2)(n+3) + 1
= n(n+3)(n+1)(n+2) + 1
= (n²+3n)(n² + 3n + 2) + 1
Khi đó, đặt x = n²+3n với x € số tự nhiên. Ta có:
A = x ( x +2) + 1 = x² + 2x + 1 = (x+1)² = (n² + 3n + 1)²
Vì n € số tự nhiên nên n² + 3n + 1 cũng là số tự nhiên.
Vì thế A = n(n+1)(n+2)(n+3) + 1 là số chính phương.
Nếu có lỡ quên số chính phương là gì thì bạn chỉ cần đọc qua bài viết trên đây là có thể dễ dàng nhớ lại phần kiến thức này. Để xác định số chính phương một cách thuần thục và chính xác nhất, bạn cần ghi nhớ các tính chất của số chính phương và thực hành giải nhiều bài tập nhé.



