Trực tâm là gì, có những tính chất gì, cách xác định trực tâm trong tam giác như thế nào? Cùng Palada.vn ôn lại nhanh kiến thức về trực tâm trong bài viết này nhé!
Tóm tắt
Trực tâm là gì?
Khái niệm trực tâm của tam giác: Nếu trong một tam giác, có ba đường cao giao nhau tại một điểm thì điểm đó được gọi là trực tâm.
- Xét trong tam giác nhọn: Trực tâm nằm ở miền trong tam giác đó.
- Xét trong tam giác vuông: Trực tâm chính là đỉnh góc vuông.
- Xét trong tam giác tù: Trực tâm nằm ở miền ngoài tam giác đó.
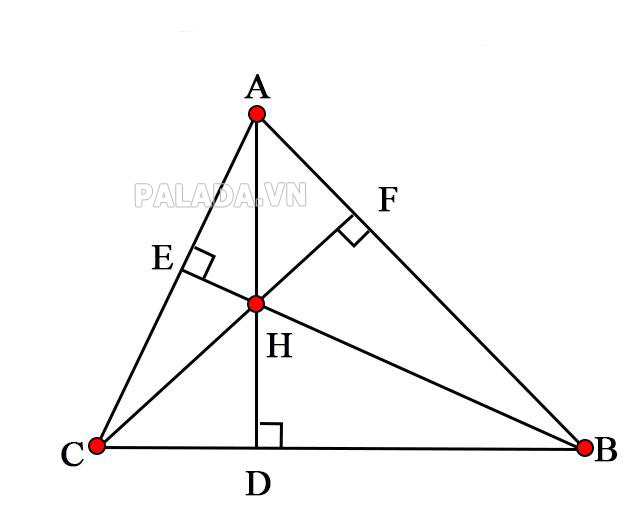
Tính chất trực tâm của tam giác
*Tính chất 1: Trong tam giác cân, đường trung trực ứng với cạnh đáy vừa đồng thời là đường phân giác, đường trung tuyến và cả đường cao của tam giác đó.
*Tính chất 2: Trong một tam giác, nếu có một đường trung tuyến cũng đồng thời là phân giác thì đó là tam giác cân.
*Tính chất 3: Trong một tam giác, nếu có một đường trung tuyến cũng đồng thời là đường trung trực thì tam giác đó là tam giác cân.
*Tính chất 4: Trực tâm của tam giác nhọn ABC trùng với tâm đường tròn nội tiếp tam giác tạo bởi 3 đỉnh là chân 3 đường cao từ các đỉnh A, B, C đến các cạnh BC, AB, AC tương ứng.
*Tính chất 5: Đường cao của tam giác tương ứng với một đỉnh cắt đường tròn ngoại tiếp tại điểm thứ hai chính là đối xứng của trực tâm qua cạnh tương ứng.
| Hệ quả: Trong một tam giác đều, trực tâm, trọng tâm, điểm cách đều 3 đỉnh, điểm nằm trong tam giác và cách đều ba cạnh chắc chắn là 4 điểm trùng nhau |
Cách xác định trực tâm của tam giác
Trực tâm của tam giác được xác định bởi giao điểm của ba đường cao trong tam giác. Tuy nhiên để tìm tọa độ trực tâm trong tam giác, chúng ta không nhất thiết phải vẽ ba đường cao. Chỉ cần vẽ hai đường cao của tam giác là đã có thể xác định được trực tâm của tam giác.
Công thức chung để xác định trực tâm của tam giác (tam giác cân, đều, tù)
Từ hai đỉnh của tam giác, kẻ hai đường cao của tam giác tới hai cạnh đối diện. Điểm giao nhau của 2 đường cao đó chính là trực tâm của tam giác. Và đường cao còn lại chắc chắn cũng sẽ đi qua trực tâm của tam giác.
Tuy nhiên đối với tam giác vuông thì việc xác định trực tâm có khác một chút. Tam giác vuông có hai cạnh góc vuông chính đồng thời là hai đường cao của tam giác. Chính vì vậy, trực tâm của tam giác vuông trùng chính là giao điểm của 2 cạnh góc vuông hay hiểu đơn giản trọng tâm chính là đỉnh của góc vuông.
Tam giác nhọn
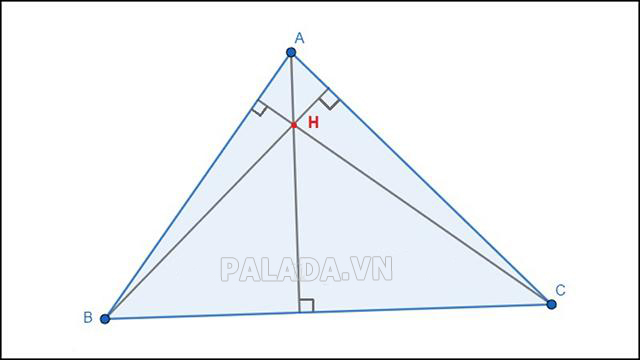
Trực tâm của tam giác nhọn nằm ở miền trong tam giác đó.
Ví dụ: Tam giác nhọn ABC có trực tâm H nằm ở miền trong của tam giác.
Tam giác vuông
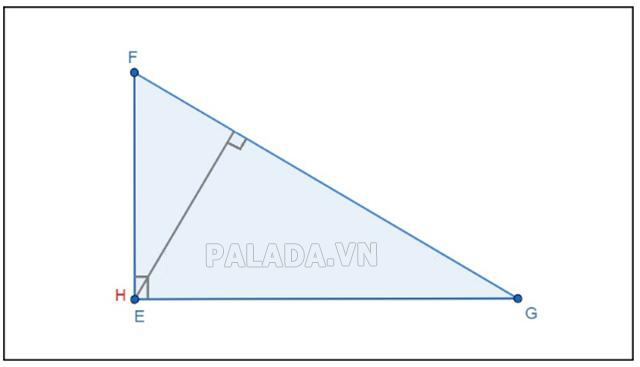
Trực tâm của tam giác vuông chính là đỉnh góc vuông.
Ví dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông tại đỉnh E.
Tam giác tù
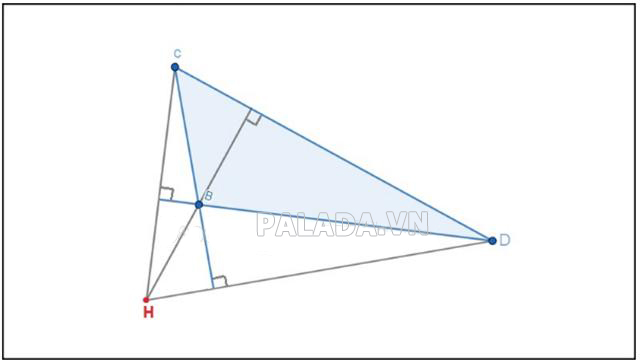
Trực tâm trong tam giác tù nằm ở miền ngoài tam giác đó.
Ví dụ: Tam giác tù BCD có điểm trực tâm H ở miền ngoài của tam giác.
Đồng quy là gì? Tính chất, chứng minh 3 đường thẳng đồng quy
Cách chứng minh trực tâm tam giác
Giả sử ta cần chứng minh G là trọng tâm, H là trực tâm ΔABC. Ta có:
Để chứng minh điểm H là trực tâm của tam giác ABC thì ta cần chứng minh điểm H là trung trực của tam giác ABC
Cách làm là hãy chứng minh H là giao điểm của hai đường cao trong tam giác.
Hy vọng với những kiến thức tổng hợp về trực tâm tam giác trong bài viết đã giúp các bạn học sinh hiểu trực tâm là gì, trực tâm của tam giác có tính chất gì, cách xác định, chứng minh trực tâm trong tam giác. Từ đó, vận dụng thuần thục vào giải các bài toán liên quan đến trực tâm của tam giác.



