Đồng quy là gì? 3 đường thẳng đồng quy là một khái niệm thường gặp trong môn toán. Dưới đây Palada.vn sẽ cùng các bạn tìm hiểu 3 đường thẳng đồng quy là gì, tính chất và cách để chứng minh 3 đường thẳng đồng quy.
Tóm tắt
3 đường thẳng đồng quy là gì?
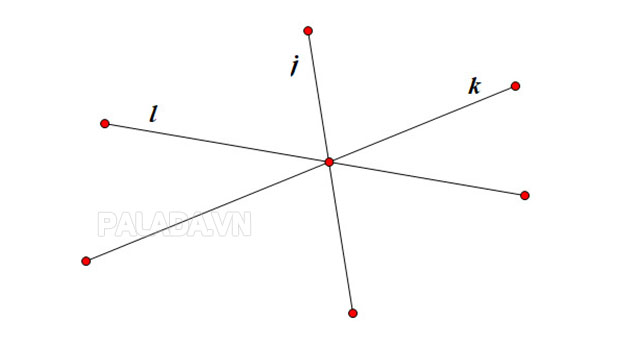
Chúng ta có ba đường thẳng l, i, k không trùng nhau. Ta nói ba đường thẳng l, i, k đồng quy khi mà ba đường thẳng đó cùng đi qua 1 điểm O nào đó.
3 đường thẳng đồng quy trong tam giác có những tính chất như sau:
– Nếu 2 đường cao trong tam giác cắt nhau tại một điểm thì từ đó suy ra đường cao thứ 3 cũng sẽ đi qua giao điểm đó.
– Ba đường trung tuyến trong một tam giác luôn đồng quy tại 1 điểm. Điểm này được gọi là điểm trọng tâm của tam giác.
– Ba đường cao trong một tam giác luôn đồng quy tại 1 điểm. Điểm này được gọi là điểm trực tâm của tam giác đó.
– Nếu hai đường trung tuyến trong tam giác cắt nhau tại 1 điểm thì suy ra đường trung tuyến thứ 3 cũng đi qua giao điểm đó. Trong tâm chia đoạn thẳng trung tuyến này thành 3 phần bằng nhau. Từ trọng tâm lên đỉnh chiếm 2/3 độ dài của trung tuyến đó.
– Ba đường phân giác trong một tam giác luôn đồng quy tại 1 điểm. Điểm này gọi là tâm của đường tròn nội tiếp của tam giác.
– Nếu hai đường phân giác trong tam giác cắt nhau tại một điểm thì đường phân giác thứ 3 cũng đi qua giao điểm đó. Giao điểm của 3 đường phân giác cách đều 3 cạnh của tam giác.
– Ba đường trung trực trong một tam giác luôn đồng quy tại 1 điểm. Điểm này gọi là tâm đường tròn ngoại tiếp của tam giác.
– Nếu hai đường trung trực trong tam giác giao nhau tại một điểm thì suy ra đường trung trực thứ 3 cũng đi qua giao điểm đó. Giao điểm của 3 đường trung trực luôn cách đều 3 đỉnh của tam giác.
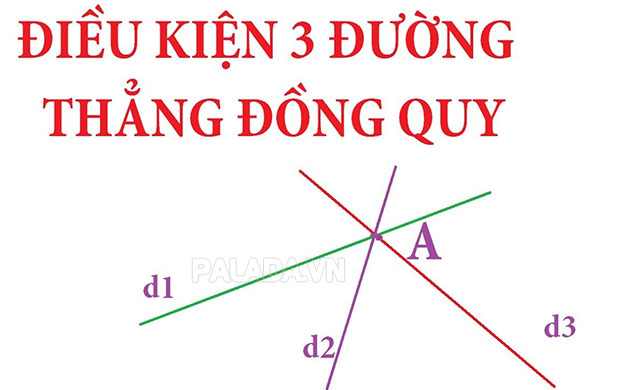
Điều kiện để có 3 đường thẳng đồng quy
Để 3 đường thẳng đồng quy thì chúng phải thỏa mãn những điều kiện sau đây:
– Định lý trọng tâm: Ba đường trung tuyến của tam giác luôn cắt nhau tại một điểm. Đồng thời khoảng cách từ điểm này đến đỉnh sẽ gấp đôi khoảng cách từ điểm này đến trung điểm của cạnh đối diện. Giao điểm nói trên gọi là trọng tâm của hình tam giác.
– Định lý tâm ngoại tiếp: các đường trung trực của ba cạnh trong một tam giác cắt nhau tại một điểm. Điểm này gọi là tâm ngoại tiếp tam giác.
– Định lý trực tâm: Ba đường cao của tam giác luôn cắt nhau tại một điểm. Điểm này sẽ gọi là trực tâm của tam giác đó.
– Định lý tâm nội tiếp: Ba đường phân giác trong của tam giác luôn cắt nhau tại một điểm. Điểm này gọi là tâm nội tuyến của tam giác đó.
– Định lý tâm bàng tiếp: Tia phân giác của góc trong của tam giác cùng tia phân giác của góc ngoài ở 2 đỉnh còn lại cắt nhau tại một điểm. Điểm này được gọi là tâm bàng tiếp của 1 tam giác. Một hình tam giác có 3 tâm bàng tiếp.
– Trọng tâm, trực tâm, tâm nội tiếp, tâm ngoại tiếp, tâm bàng tiếp đều là tâm của tam giác. Chúng đều có những mối liên hệ quan trọng với hình tam giác.
Tính chất đường trung trực của tam giác, định nghĩa và bài tập
Cách chứng minh 3 đường thẳng đồng quy
Trong các bài toán hình học phẳng ở cấp THCS, để chứng minh 3 đường thẳng đồng quy thì chúng ta có thể sử dụng một số phương pháp sau đây :
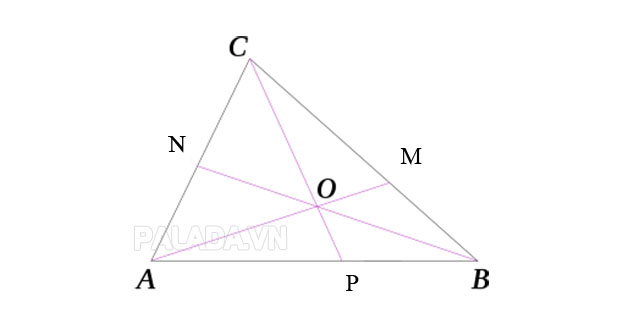
– Sử dụng định lý Ceva: Cho tam giác ABC cùng ba điểm bất kì M, N, P nằm trên ba cạnh BC, CA, AB. Ta có ba đường thẳng AM, BN, CP là đồng quy khi và chỉ khi:
MB⁄MC.NC⁄NA.PA⁄PB = 1
– Tìm giao điểm của hai đường thẳng, sau đó chứng minh đường thẳng thứ ba cũng đi qua giao điểm đó.
– Sử dụng tính chất 3 đường đồng quy trong tam giác:
+ Ba đường trung tuyến của tam giác luôn đồng quy tại trọng tâm tam giác.
+ Ba đường phân giác luôn đồng quy tại tâm đường tròn nội tiếp tam giác.
+ Ba đường trung trực luôn đồng quy tại tâm đường tròn ngoại tiếp tam giác.
+ Ba đường cao luôn đồng quy tại trực tâm tam giác.
– Đặc biệt ba điểm trọng tâm, trực tâm và tâm của đường tròn ngoại tiếp thẳng hàng nhau. Đường thẳng đi qua ba điểm đó sẽ được gọi là đường thẳng Euler của tam giác.
Trên đây là những kiến thức cơ bản giúp các bạn và các em học sinh hiểu hơn về 3 đường thẳng đồng quy là gì. Nếu còn gì thắc mắc về nội dung này, hãy để lại bình luận bên dưới để được chúng mình giải đáp nhanh nhất nhé.



