Trong hình học, đường trung tuyến là một loại đường thẳng quan trọng với các bài toán về tam giác. Vậy đường trung tuyến của tam giác là đường gì? Hãy cùng chúng tôi tìm hiểu thêm về tính chất, định nghĩa và công thức tính đường thẳng này trong bài viết này.
Tóm tắt
Định nghĩa đường trung tuyến trong tam giác là gì?
Đoạn thẳng nối một đỉnh với trung điểm của cạnh đối diện với đỉnh đó gọi là đường trung tuyến của một tam giác. Trong hình dưới đây, AD là trung tuyến chia BC thành hai phần sao cho BD = DC.
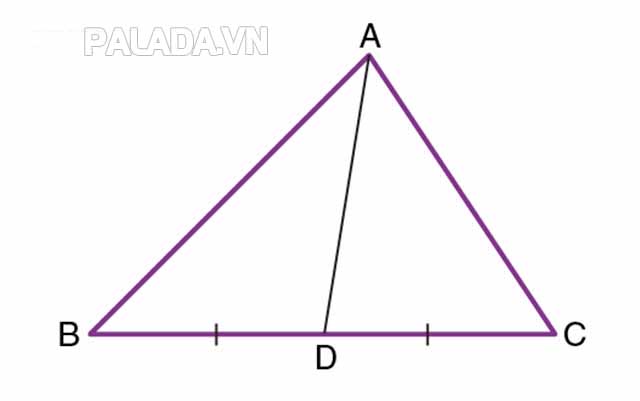
Tính chất đường trung tuyến trong một tam giác là gì?
Các đường trung tuyến trong một tam giác có những tính chất cơ bản sau:
- Trung tuyến của tam giác là đoạn thẳng nối đỉnh của nó với trung điểm của cạnh đối diện, do đó nằm trên đường thẳng đi qua trung điểm của cạnh đối diện.
- Đường trung tuyến của một tam giác chia tam giác đó thành hai tam giác có cùng diện tích.
- Ba đường trung tuyến của mọi tam giác gặp nhau tại một điểm duy nhất. Giao điểm của 3 trung tuyến tạo thành trọng tâm của tam giác.
- Trọng tâm chia chiều dài của mỗi trung tuyến theo tỷ lệ 2:1. Độ dài của phần giữa đỉnh và trọng tâm gấp đôi độ dài giữa trọng tâm và trung điểm của cạnh đối diện.
- Mỗi trung tuyến của một tam giác chia tam giác đó thành hai tam giác nhỏ có diện tích bằng nhau. Vậy 3 đường trung tuyến chia tam giác đó thành 6 tam giác nhỏ có diện tích bằng nhau.
Đường trung tuyến trong các loại tam giác
Ngoài những tính chất chung ở trên, đường trung tuyến trong mỗi loại tam giác đặc biệt lại có những tính chất riêng khác nhau.
Đường trung tuyến trong tam giác vuông có tính chất là gì?
Trong một tam giác vuông, đường trung tuyến có các tính chất đặc biệt như sau:
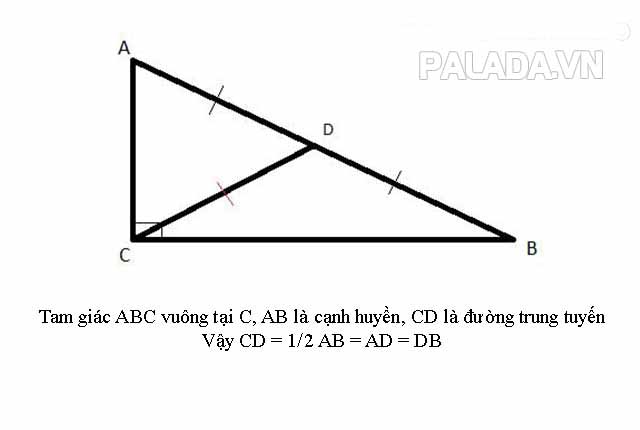
- Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền sẽ có độ dài bằng 1/2 độ dài cạnh huyền.
- Một tam giác là tam giác vuông nếu trung tuyến của cạnh huyền bằng nửa độ dài cạnh đó.
- Trong một tam giác vuông, tổng bình phương độ dài các đường trung tuyến đi qua trung điểm hai cạnh góc vuông bằng 5/4 bình phương độ dài cạnh huyền.
Đường trung tuyến trong tam giác cân có tính chất gì?
Đường trung tuyến trong tam giác cân có các tính chất khác như sau:
- Độ dài hai đường trung tuyến đi qua trung điểm của hai cạnh bên bằng nhau sẽ bằng nhau.
- Đường trung tuyến đi qua trung điểm của cạnh đáy tam giác cân vừa là đường cao, vừa là đường phân giác trong tam giác.
Đường trung tuyến trong tam giác đều có tính chất gì?
Đường trung tuyến trong tam giác đều có các tính chất khác cần ghi nhớ như sau:
- Ba đường trung tuyến của tam giác đều sẽ có độ dài bằng nhau.
- Ba đường trung tuyến của tam giác đều vừa là đường trung tuyến, vừa là đường cao, vừa là đường phân giác của các góc trong tam giác.
- Do đó, giao điểm của ba đường trung tuyến vừa là trọng tâm, vừa là trực tâm, vừa là tâm đường tròn nội tiếp tam giác.
Cách tính độ dài đường trung tuyến là gì?
Theo định lý đường trung tuyến trong tam giác của Apollonius, tổng bình phương của một trong hai cạnh bất kỳ trong tam giác bằng hai lần bình phương của nó trên một nửa cạnh thứ ba, cùng với hai lần bình phương của nó trên đường trung tuyến chia đôi cạnh thứ ba.
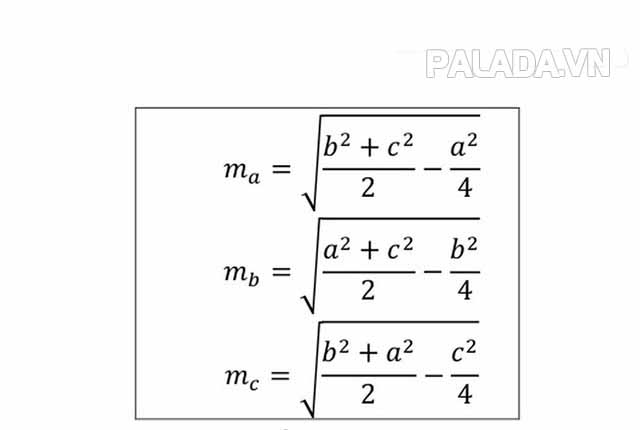
Từ định lý trên, chúng ta có công thức tính độ dài đường trung tuyến là:
Xem thêm:
Trong đó: a, b, c là ba cạnh của tam giác.
ma, mb, mc lần lượt là các đường trung tuyến ứng với các cạnh a, b, c.
Cách tính độ dài đường trung tuyến trong tam giác có tọa độ
Khi biết tọa độ ba đỉnh của một tam giác, chúng ta có thể làm theo các bước dưới đây để tìm độ dài đường trung tuyến của tam giác.
- Bước 1: Dựa vào tọa độ các đỉnh của tam giác, tìm tọa độ trung điểm của đoạn thẳng tạo thành đường trung tuyến. Sử dụng công thức trung điểm là: [(x1 + x2 )/2, (y1 + y2 )/2], trong đó (x1 , y1 ) và (x2 , y2 ) là tọa độ của hai điểm của cạnh chứa trung điểm.
- Bước 2: Sau khi có được tọa độ của trung điểm, hãy tìm độ dài của đường trung tuyến bằng cách sử dụng công thức khoảng cách, trong đó một điểm là đỉnh nơi đường trung tuyến bắt đầu và điểm còn lại là trung điểm.
- Bước 3: Độ dài đường trung tuyến có thể được tính bằng công thức khoảng cách, D= √[(x2 – x1 ) 2 + (y2 – y1 ) 2 ]; trong đó (x1 , y1 ) và (x1 , y1 ) là tọa độ của trung tuyến.
Bài viết đã giải đáp những thắc mắc về đường trung tuyến trong tam giác là gì, đường trung tuyến có những tính chất như thế nào? Vấn đề về đường trung tuyến là một trong những vấn đề được ứng dụng nhiều trong nghiên cứu về tam giác và những định lý, bài toán liên quan đến tam giác. Hy vọng sau khi đọc xong bài viết, bạn đã có thêm nhiều kiến thức bổ ích về vấn đề này.



