Số thực là gì? Gồm những số nào? Tính chất và ví dụ về số thực

Toán học là một trong những môn học bắt buộc mà chúng ta đã học từ khi còn nhỏ. Bộ môn này có rất nhiều ứng dụng trong cuộc sống và một trong đó là số thực. Vậy số thực là gì? Cùng Palada.vn củng cố lại kiến thức trong bài viết sau nhé.

Khái niệm số thực là gì?

Số thực là gì?

Số thực là tập hợp số bao gồm các số nguyên dương (ví dụ 1, 2, 3,…), số 0, số nguyên âm (ví dụ -1, -2, -3,…), số hữu tỉ (ví dụ 5/2, -2/3), số vô tỉ (ví dụ số pi, số √2). Số thực có thể được xem như là các điểm nằm trên một trục số dài vô hạn.

Tập hợp số thực là gì, kí hiệu như thế nào? Tập số thực kí hiệu là R. Số thực là tập hợp các số hữu tỉ và số vô tỉ: R = Q ∪ I.

Số thực bao gồm các số thực âm, số 0 và số thực dương.

Như vậy, ta có số thực bao gồm:

• Tập hợp số tự nhiên kí hiệu là N: N = {0, 1, 2, 3,…}
• Tập hợp các số nguyên kí hiệu là Z: Z = {…, -3, -2, -1, 0, 1, 2, 3,…}
• Tập hợp các số hữu tỉ Q: Q = {x = a/b; a, b ϵ Z, b ≠0}
• Tập hợp các số vô tỉ I: I ={các số thập phân vô hạn không có tuần hoàn, ví dụ như √2, số pi}

Số thực là gì ví dụ?

Các ví dụ về số thực đó là:

• Số tự nhiên: 1, 6, 3, 4, 5,…
• Số nguyên: −17, -2, 3, 8,…
• Số hữu tỉ: 4/3, 7/10,…
• Số vô tỉ: √2 = 1,41421356…; pi = 3,1456…,….

Trục số thực là gì?

Trục số thực là một trục nằm ngang để biểu diễn tập hợp R của các số thực. Mỗi số thực đều có thể được biểu diễn bằng 1 điểm trên trục số.

Ngược lại, mỗi điểm trên trục số lại biểu diễn cho một số thực. Chỉ có tập hợp R số thực mới có thể lấp đầy trục số đó.

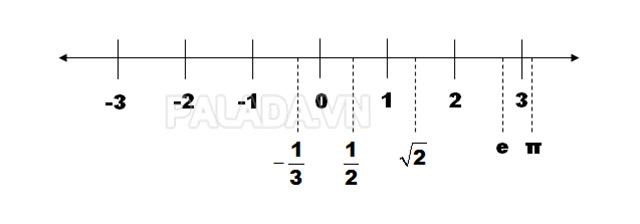
Trong tập hợp số thực R, ta cũng định nghĩa về các phép toán lũy thừa, cộng, trừ, nhân, chia, căn,…Và trong các phép toán này, các số thực cũng có các tính chất như các phép toán trong tập hợp số hữu tỉ.

Tính chất số thực là gì?

Tính chất của các số thực:

• Bất kỳ số thực nào ≠ 0 thì nó sẽ là số âm hoặc dương.
• Tổng hoặc tích của hai số thực không phải âm là một số thực không âm.
• Số thực là tập hợp vô hạn các số nên không đếm được các số thực.
• Số thực có hệ thống các tập hợp con là vô hạn có thể đếm được.
• Số thực có thể biểu thị bằng thập phân.
• Số thực có thể được dùng để thể hiện các phép đo đại lượng liên tục.

Thuộc tính số thực là gì?

Số thực có hai thuộc tính cơ bản đó là thuộc tính cận trên thấp nhất và thuộc tính trường có thứ tự.

Thuộc tính cận trên thấp nhất

Thuộc tính này chỉ ra nếu tập hợp một số thực không trống có giới hạn trên thì nó có cận trên là những số thực nhỏ nhất.

Thuộc tính trường có thứ tự

Thuộc tính này chỉ ra rằng các số thực bao gồm một trường, với các phép cộng và phép nhân cùng phép chia cho các số khác không. Chúng có thể được sắp xếp hoàn toàn trên một trục số theo cách tương thích với phép cộng, phép nhân.

Tập hợp số thực là gì?

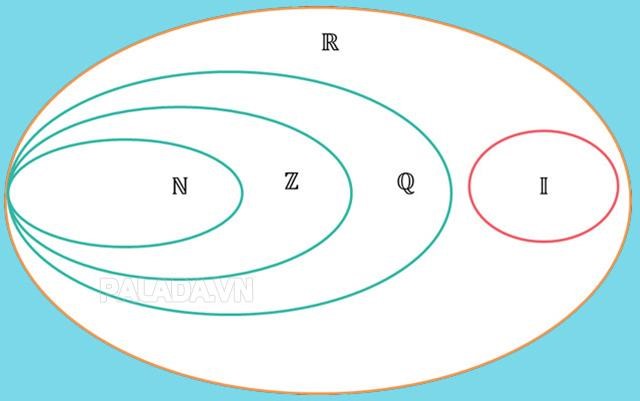
Kí hiệu của tập số thực là R. Số thực gồm có số hữu tỉ, số vô tỉ.

• Số hữu tỉ là số viết được dưới dạng phân số phân số a/b (với a, b ∈ Z, b ≠ 0). Tập hợp các số hữu tỉ là Q.

Ví dụ: −3/5; 4/3,…

• Số vô tỉ là số thập phân vô hạn không quy luật, tuần hoàn. Tập số vô tỉ được kí hiệu là I.

Ví dụ: √2; pi = 3,1415…

Ta có: N ⊂ Z ⊂ Q, cho nên suy ra R = Q ∪ I.

Sự khác nhau giữa số thực là gì số nguyên là gì?

Số nguyên là gì?

Số nguyên là tập hợp số bao gồm số 0, các số tự nhiên dương và các số tự nhiên âm. Tập hợp số nguyên tuy vô hạn nhưng có thể đếm được.

Số nguyên được chia làm hai loại là nguyên dương và nguyên âm. Kí hiệu của tập hợp số nguyên là Z.

Sự khác nhau giữa số thực là gì số nguyên là gì?

Sự khác nhau giữa các số nguyên và các số thực là:

• Số thực là tập hợp các số không thể đếm được.
• Số nguyên là tập hợp các số có thể đếm được.
• Số nguyên là một trong các tập hợp con của số thực.

Bài tập về số thực là gì

Dạng 1: Hỏi về các tập hợp số

Phương pháp: Sử dụng kí hiệu về tập hợp số. Trong đó:

• N: Là tập các số tự nhiên
• Z: Là tập các số nguyên
• Q: Là tập các số hữu tỉ
• I: Là tập các số vô tỉ
• R: Là tập các số thực

Ta có quan hệ giữa các tập hợp số này như sau: N ⊂ Z ⊂ Q ⊂ R; và I ⊂ R.

Dạng 2: Tìm số còn chưa biết trong một đẳng thức

Phương pháp:

• Áp dụng từ tính chất của các phép toán.
• Áp dụng quan hệ giữa các số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong 1 tích; quan hệ giữa số bị chia, số chia, thương số trong phép chia.
• Áp dụng quy tắc chuyển vế, phá dấu ngoặc.

Dạng 3: Tính giá trị một biểu thức

Phương pháp:

• Thực hiện các phép tính có trong biểu thức như cộng, trừ, nhân, chia và lũy thừa. Cần lưu ý đến thứ tự thực hiện phép tính: nhân chia trước, cộng trừ sau.
• Rút gọn các phân số nếu như có thể.
• Vận dụng các tính chất khác của phép toán sao cho thích hợp.

Số hạng là gì? Ví dụ và bài tập về số hạng – tổng Toán 2

Qua bài viết vừa rồi Palada.vn hi vọng đã giúp bạn hiểu được khái niệm số thực là gì, kí hiệu và các ví dụ của nó. Hãy luyện tập thật nhiều để nắm vững kiến thức này các bạn nhé.