Tuyến tính là khái niệm được sử dụng trong nhiều lĩnh vực. Tuyến tính là gì? Ý nghĩa của tuyến tính là gì trong các lĩnh vực đời sống? Cùng palada.vn tìm hiểu về khái niệm tuyến tính và phi tuyến tính qua bài viết này nhé.
Tóm tắt
Tuyến tính là gì?
Tuyến tính là một thuộc tính hoặc quan hệ mà có tính chất thẳng hàng, không cong. Trong ngữ cảnh toán học, tuyến tính đề cập đến các phương trình, hàm số hoặc quan hệ tuyến tính.

Phương trình hoặc hàm số tuyến tính là một phương trình hoặc hàm số có dạng tuyến tính, tức là hàm bậc nhất. Nó thường được biểu diễn dưới dạng tổng các thành phần tuyến tính, trong đó mỗi thành phần được nhân với một hệ số và cộng với một số hạng tự do.
Ví dụ về phương trình tuyến tính là ax + by + c = 0, trong đó a, b và c là các hệ số & x, y là các biến. Đây là một phương trình tuyến tính vì mỗi biến có bậc một và không có một biểu thức mũ hay căn bậc hai.
Tuyến tính cũng ám chỉ một thuộc tính của các quan hệ giữa các biến. Nếu một quan hệ giữa các biến có tính chất thẳng hàng, tức là nó có thể biểu diễn bằng một phương trình hoặc hàm số tuyến tính, thì quan hệ đó được gọi là tuyến tính. Quan hệ tuyến tính thường được xác định bởi độ dốc (hệ số góc) và điểm giao với trục hoành (hệ số điều chỉnh).
Tính tuyến tính có ứng dụng rộng rãi trong nhiều lĩnh vực như đại số tuyến tính, hình học, kinh tế học, vật lý, thống kê và các lĩnh vực kỹ thuật khác.
Tuyến tính và phi tuyến tính là gì?
Trong toán học và khoa học máy tính, các thuật ngữ “tuyến tính” và “phi tuyến tính” được sử dụng để miêu tả tính chất của một hàm hoặc một mô hình.
Tuyến tính là gì?
Một hàm được gọi là tuyến tính nếu nó thỏa mãn hai tính chất sau:
– Tính chất cộng dồn: Khi áp dụng phép toán cộng hai đầu vào, kết quả của hàm với tổng đầu vào bằng tổng kết quả của hàm với từng đầu vào riêng lẻ. Nói cách khác, đường cong biểu diễn hàm là một đường thẳng.
– Tính chất nhân theo hằng số: Khi nhân đầu vào của hàm với một hằng số, kết quả của hàm nhân với hằng số đó bằng kết quả của hàm với đầu vào ban đầu nhân với hằng số đó. Nói cách khác, đường cong biểu diễn hàm là một đường thẳng đi qua gốc tọa độ.
Ví dụ về hàm tuyến tính: f(x) = ax + b, trong đó a và b là các hằng số.
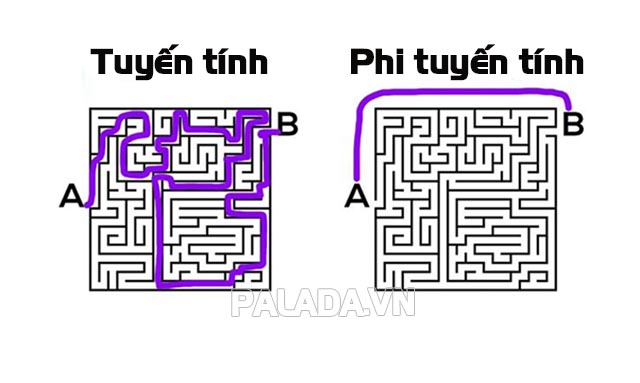
Phi tuyến tính là gì?
Một hàm được gọi là phi tuyến tính nếu nó không thỏa mãn cả hai tính chất được đề cập ở trên. Điều này có nghĩa rằng đường cong biểu diễn hàm không phải là một đường thẳng.
Ví dụ về hàm phi tuyến tính: f(x) = x^2, f(x) = sin(x), f(x) = e^x, trong đó x^2 là hàm bậc hai, sin(x) là hàm sin, và e^x là hàm mũ.
Một trong những khác biệt chính giữa các hàm tuyến tính và phi tuyến tính là tính chất của sự biến đổi giữa đầu vào và đầu ra. Trong hàm tuyến tính, sự biến đổi giữa đầu vào và đầu ra là tuyến tính, trong khi trong hàm phi tuyến tính, sự biến đổi này có tính phi tuyến.
Quan hệ tuyến tính là gì?
Quan hệ tuyến tính là một loại quan hệ giữa hai biến trong toán học, trong đó mối quan hệ giữa chúng có thể được mô tả bằng một phương trình tuyến tính. Một phương trình tuyến tính là một phương trình trong đó mỗi biến có bậc là 1, tức là không có một biến nào được nhân với chính nó hoặc có các mũ khác nhau.
Trong mô hình tuyến tính, biến độc lập (thường được ký hiệu là x) được giả định ảnh hưởng tuyến tính đến biến phụ thuộc (thường được ký hiệu là y). Một mô hình tuyến tính có thể được biểu diễn bằng một phương trình tuyến tính đơn giản như sau:
y = a * x + b
Trong đó, a và b là các hằng số và có thể được xác định bằng cách sử dụng các phương pháp như phương pháp bình phương tối thiểu hoặc phương pháp hồi quy tuyến tính.
Mối quan hệ tuyến tính được sử dụng rộng rãi trong các lĩnh vực như toán học, kinh tế, khoa học dữ liệu và kỹ thuật. Nó cung cấp một công cụ mạnh mẽ để mô hình hóa và dự đoán các mối quan hệ giữa các biến và có thể giúp trong việc giải quyết các bài toán phức tạp.
Dãy số tuyến tính là gì?
Dãy số tuyến tính là một loại dãy số trong đó mỗi số hạng được tính bằng cách thêm một số hạng cố định vào số hạng trước đó.
Ví dụ, nếu ta có một dãy số tuyến tính bắt đầu từ 2 và có công sai là 3, ta có thể tính các số hạng như sau:
a₁ = 2
a₂ = a₁ + 3 = 2 + 3 = 5
a₃ = a₂ + 3 = 5 + 3 = 8
a₄ = a₃ + 3 = 8 + 3 = 11
và cứ tiếp tục như vậy.
Dãy số tuyến tính thường được sử dụng nhiều trong toán học và khoa học, và chúng có các ứng dụng rộng rãi trong các lĩnh vực như chuỗi số, dãy số số nguyên, tài chính,…
Đường tuyến tính là gì?
Đường tuyến tính là một khái niệm quan trọng trong đại số tuyến tính và hình học. Nó là một đường thẳng trong không gian hai chiều hoặc không gian ba chiều (và có thể mở rộng ra không gian nhiều chiều hơn) được biểu diễn bằng phương trình tuyến tính.
Trong không gian hai chiều, một đường tuyến tính có thể được biểu diễn bằng phương trình đường thẳng y = mx + b, trong đó m là hệ số góc của đường thẳng và b là hệ số điều chỉnh đường thẳng (hoặc hệ số giao điểm của đường thẳng với trục y).
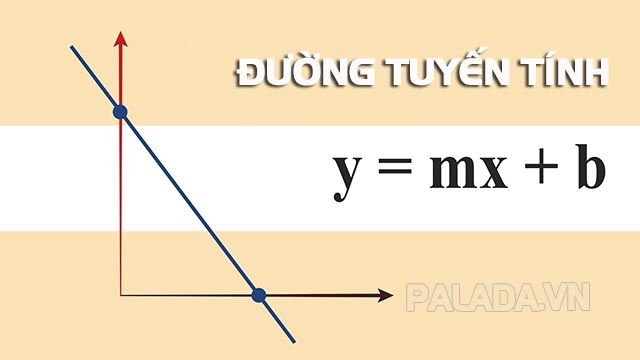
Trong không gian ba chiều, một đường tuyến tính được biểu diễn bằng phương trình chung của mặt phẳng ax + by + cz + d = 0, trong đó a, b, c là các hệ số xác định hướng của mặt phẳng và d là hệ số điều chỉnh.
Đường tuyến tính có nhiều ứng dụng trong các lĩnh vực như đại số tuyến tính, hình học, và kỹ thuật. Nó được sử dụng để mô hình hóa các quan hệ tuyến tính giữa các biến và giúp giải quyết các bài toán liên quan đến tìm kiếm điểm giao của các đường tuyến tính hoặc mặt phẳng.
Hàm số tuyến tính là gì?
Hàm số tuyến tính là một loại hàm số trong toán học mô tả một quan hệ tuyến tính giữa biến độc lập và biến phụ thuộc. Nó có dạng chung là f(x) = mx + b, trong đó m là hệ số góc và b là hệ số điều chỉnh.
Trong hàm số tuyến tính, biến độc lập thường được ký hiệu là x, trong khi biến phụ thuộc được ký hiệu là f(x) hoặc y. Hệ số góc m biểu thị độ dốc của đường thẳng và chỉ ra mức độ thay đổi của f(x) khi x thay đổi. Hệ số điều chỉnh b là giá trị của f(x) khi x = 0, nó xác định vị trí của đường thẳng trên trục y.
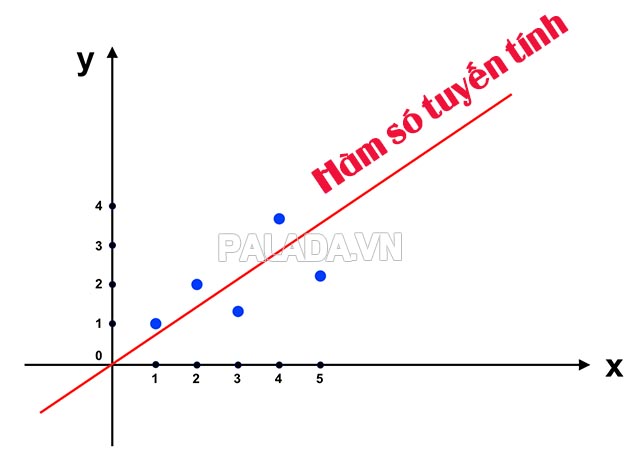
Hàm số tuyến tính có đặc điểm là đồ thị của nó là một đường thẳng. Đường thẳng này có thể có độ dốc dương (khi m > 0), độ dốc âm (khi m < 0) hoặc là một đường thẳng ngang (khi m = 0). Hàm số tuyến tính cũng có thể có độ dốc vô cùng (khi m không xác định) và đường thẳng song song với trục x.
Hàm số tuyến tính được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm đại số tuyến tính, kinh tế học, thống kê, và các lĩnh vực kỹ thuật khác. Nó cung cấp một phương pháp đơn giản để mô hình hóa và dự đoán các quan hệ tuyến tính giữa các biến.
Vậy là bài viết đã giải đáp những thông tin về khái niệm tuyến tính là gì và ý nghĩa của tuyến tính trong các lĩnh vực. Vì tuyến tính là một khái niệm trừu tượng nên bạn cần vận dụng vào thực tế để hiểu rõ hơn về khái niệm này.



