R tập hợp số thực là khái niệm quen thuộc trong môn toán tuy nhiên không phải ai cũng có thể nắm vững. Trong bài viết này Palada.vn sẽ cùng các bạn tìm hiểu về r là tập hợp số gì, ví dụ, những khái niệm cơ bản về số thực, các tính chất để các bạn hiểu rõ hơn vai trò của số thực trong Toán học như thế nào. Hãy cùng theo dõi nhé.

Tóm tắt
Số thực R là gì?
R là tập hợp số nào? R tập hợp số thực bao gồm tất cả các số hữu tỉ, như số nguyên − 6 và phân số 8/3 cùng tất cả các số vô tỉ, chẳng hạn như √2 = 1.41421356… và số 0.
Hoặc một cách định nghĩa R tập hợp số thực chính là tập hợp bao gồm số dương (ví dụ như 1, 2, 3, 4…), số 0, số âm (-1, -2, -3, -4…), các số vô tỉ cùng các số hữu tỉ. R tập hợp số thực có thể được xem là các điểm nằm trên một trục số dài vô hạn.
Số 0 cũng là một số thực vì nó thuộc tập hợp số nguyên dù không phải số nguyên âm cũng không phải số nguyên dương, mà số nguyên là tập con của R nên số 0 vẫn thuộc R.
Tính chất của tập số thực R

– Bất kỳ số thực nào khác không thì sẽ là một số âm hoặc một số dương.
– Tổng/tích của hai số thực không âm thì cũng là một số thực không âm.
– Số thực là tập hợp vô hạn, chúng ta không thể nào đếm được các số thực.
– Tồn tại hệ thống các tập con vô hạn có thể đếm được của các số thực R (R = Q U I)
Trong đó:
N: Tập hợp các số tự nhiên
Z: Tập hợp các số nguyên
Q: Tập hợp số hữu tỉ
I = RQ: Tập hợp các số vô tỉ
– Số thực có thể được sử dụng trong việc thể hiện các phép đo đại lượng liên tục.
– Số thực có thể biểu thị bằng cách biểu diễn thập phân.
Trục R tập hợp số thực
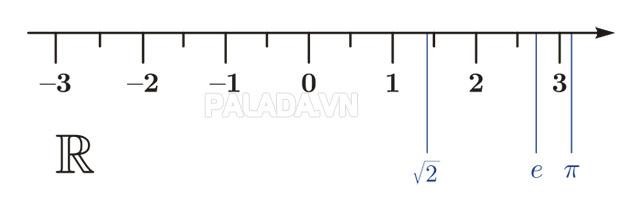
Mối số thực được biểu diễn bởi một điểm trên trục số và ngược lại, mỗi điểm trên trục số sẽ biểu diễn một số thực. Chỉ có tập hợp số thực R mới có thể lấp đầy trục số.
Trong R tập hợp số thực, ta cũng có các phép toán cộng trừ, nhân, chia, lũy thừa, căn bậc… Trong các phép toán với số thực cũng có các tính chất như phép toán trong tập hợp các số hữu tỉ.
Ta có: N ⊂ Z ⊂ Q ⊂ R.
Các thuộc tính của số thực R
Ký hiệu R trong toán học được hiểu là R tập hợp số thực và chúng có các thuộc tính là:
– R cho biết các số thực bao gồm một trường, với phép cộng, phép nhân cùng phép chia cho các số khác 0. Chúng có thể sắp xếp trên một trục hoành theo cách tương thích với phép cộng và phép nhân.
– Tập R cho biết nếu tập hợp một số thực không rỗng có giới hạn trên thì nó có cận trên là những số thực nhỏ nhất.
Ứng dụng của tập hợp số thực R
Với những tính chất bên trên thì liệu có ứng dụng nào của tập hợp số thực R hay không, hãy cùng tiếp tục theo dõi nhé.
Số thực R và logic
Các số thực R thường được chuẩn tắc hóa bằng tiên đề Zermelo-Fraenkel của lý thuyết tập hợp, nhưng một số nhà toán học nghiên cứu R bằng các cơ sở logic khác của toán học. Đặc biệt, các số thực R còn được nghiên cứu trong toán học kiến thiết và toán học đảo ngược.
Ứng dụng R tập hợp số thực vật lý
Trong ngành khoa học vật lý, hầu hết các hằng số vật lý như vị trí, diện tích, khối lượng… đều có thể được mô hình hóa bằng cách sử dụng số thực.
Trong tính toán
Hầu hết các máy tính không hoạt động dựa trên số thực. Thay vào đó, chúng hoạt động với các phép tính xấp xỉ chính xác hữu hạn.
Máy tính không thể lưu trữ trực tiếp các số thực có vô số chữ số. Tuy nhiên, các hệ thống máy tính có thể hoạt động chính xác trên các đại lượng vô tỉ bằng cách thao tác các công thức cho chúng. Số thực chỉ có thể được tính toán chứ không thể đếm được vì nhiều số thực có số chữ số là vô hạn.
Số thực là gì? Gồm những số nào? Tính chất và ví dụ về số thực
Như vậy từ nay khi một ai đó hỏi bạn R là tập hợp số gì thì với những kiến thức trong bài viết này chắc chắn sẽ giúp bạn trả lời chính xác câu hỏi đó. Hi vọng các bạn có thể nắm rõ các kiến thức về R là tập hợp số nào trong toán học để có thể áp dụng giải các bài tập nhanh gọn và dễ dàng hơn.



