Tam giác là dạng hình học phổ biến nhất trong chương trình Toán hình học ở các khối lớp phổ thông. Cách tính chu vi tam giác là dạng bài tập cơ bản và đơn giản nhất trong những dạng bài toán về tam giác. Trong thời gian học online do dịch bệnh này, các vị phụ huynh hãy giúp con em mình ôn lại kiến thức này thông qua bài viết dưới đây của Palada.vn nhé.
Tóm tắt
Chu vi tam giác là gì?
Chu vi tam giác nói theo cách đơn giản nhất chính là độ dài đường bao quanh một hình tam giác.
Tính chu vi tam giác ABC thế nào?
Quy tắc tính chu vi hình tam giác như sau:
P = a + b + c
Trong đó: P gọi là chu vi hình tam giác.
a, b, c lần lượt là 3 cạnh của hình tam giác đó.
Có thể phát biểu bằng lời như sau: Muốn tính chu vi của một hình tam giác, ta hãy cộng độ dài ba cạnh của tam giác đó với nhau.
Thường thì các em học sinh sẽ được làm quen với dạng bài tập tính chu vi hình tam giác lớp 2. Cho đến toán lớp 3 tính chu vi hình tam giác vẫn là 1 dạng toán phổ biến. Tuy nhiên bài tập về cách tính chu vi hình tam giác lớp 5 hay thậm chí là tính chu vi tam giác ABC lớp 10 cũng có, với các mức độ khó tăng dần.
Một số bài tập tính chu vi tam giác:
– Dạng 1: Tìm chu vi tam giác đã biết độ dài 3 cạnh.
Cách làm : Ta chỉ cần áp dụng quy tắc tính chu vi hình tam giác, thay số và tính toán là tìm ra chu vi.
– Dạng 2: Cho độ dài 2 cạnh và 1 góc được tạo bởi 2 cạnh đó. Tính chu vi tam giác.
Cách làm:
Bước 1: Tìm độ dài cạnh còn lại bằng cách dùng định lí Cosin
Gọi tam giác ABC có độ dài các cạnh là: AB, AC, BC:
Ta có:
Tính AB: AB2 = BC2 + AC2 – 2 * BC * AC * cosC
=> AB = √(BC2 + AC2 – 2 * BC * AC * cosC)
Tính AC: AC2 = AB2 + BC2 – 2 * AB * BC * cosB
=> AC = √(AB2 + BC2 – 2.AB * BC * cosB)
Tính BC: BC2 = AB2 + AC2 – 2 * AB * AC * cosA
=> BC = √(AB2 + AC2 – 2 * AB * AC * cosA)
Bước 2: Thay các đại lượng đã biết vào quy tắc tính chu vi hình tam giác để tìm ra kết quả.
* Cụ thể: Tam giác ABC có độ dài các cạnh AB = 7 cm, BC = 6 cm, góc ABC = 60 độ. Tính P tam giác ABC.
Giải: Áp dụng định lí Cosin, ta có:
AC = √(AB2 + BC2 – 2 * AB * BC * cosB)
=> AC = √(72 + 62 – 2 * 7 * 6 * cos60)
=> AC = √(72 + 62 – 2 * 7 * 6 * 0,5)
=> AC = √43 = 6,5 (cm)
Vậy ta có chu vi tam giác ABC là: 7 + 6 + 6,5 = 19,5 (cm)
– Dạng 3: Biết bán kính của đường tròn nội tiếp và diện tích của tam giác, tìm chu vi của tam giác thường.
Cách làm :
Bước 1: Tính 1 nửa chu vi của tam giác
Ta tính nửa P tam giác bằng cách sử dụng công thức tính S tam giác ngoại tiếp đường tròn: S = p * r => p = S / r
Với: S là kí hiệu của diện tích tam giác.
p là kí hiệu của nửa chu vi tam giác.
r: bán kính đường tròn nội tiếp.
Bước 2: Tính chu vi tam giác
Áp dụng công thức: P = p * 2 (Với P là chu vi tam giác)
* Cụ thể: Tam giác ABC ngoại tiếp đường tròn có r = 4 cm và diện tích tam giác = 30 cm2. Tính P của tam giác thường.
Lời giải:
Nửa chu vi của tam giác là: 30/4 = 7,5 (cm)
Chu vi hình tam giác là: 7,5 * 2 = 15 (cm)
Đáp số: 15 cm.
Quy tắc tính chu vi tam giác vuông
Tam giác vuông là khái niệm hình học khá quen thuộc với những ai đã gắn bó với bộ môn Toán. Trong đó cách tính chu vi tam giác vuông cũng có sự khác biệt so với cách tính chu vi các loại tam giác khác. Đây cũng là kiến thức cần thiết mà chúng ta nên biết để áp dụng vào cuộc sống.
Quy tắc tính chu vi hình tam giác vuông:
Nếu như chu vi tam giác tính bằng độ dài các cạnh của hình tam giác thì chu vi của tam giác vuông được tính bằng công thức sau:
P = a + b + h
Trong đó: P là ký hiệu của chu vi tam giác.
a, b là các cạnh bên tạo thành góc vuông của tam giác.
h là cạnh huyền.
– Cạnh huyền chính là cạnh đối diện với góc vuông.
– Hai cạnh còn lại gọi là cạnh kề (hay còn gọi là cạnh góc vuông) của tam giác vuông.
Các bài toán về chu vi tam giác vuông
Bài toán 1: Nếu đề bài toán đã cho sẵn độ dài của ba cạnh trong tam giác vuông, ta chỉ cần áp dụng quy tắc tính chu vi hình tam giác vuông: P = a + b + h rồi thay các dữ kiện vào là tính xong.
Bài toán 2: Muốn tính được chu vi tam giác vuông khi chỉ biết độ dài 2 cạnh, ta cần phải sử dụng Định lí Pytago. Định lí này do nhà Toán học người Hy Lạp tên là Pytago sáng tạo ra, dựa trên mối quan hệ của 3 cạnh trong một tam giác vuông, được phát biểu như sau: Bình phương của cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương hai cạnh còn lại (cạnh kề).
Công thức Pytago : a2 + b2 = c2
Trong đó có: a, b là độ dài của hai cạnh góc vuông (cạnh kề)
c là độ dài của cạnh huyền.
Như vậy, trong bài toán kiểu này, ta thực hiện theo hai bước:
– Bước 1: Áp dụng định lý Pytago tính cạnh còn lại chưa biết.
– Bước 2: Áp dụng quy tắc tính chu vi hình tam giác vuông để tìm ra đáp án chính xác nhất.
Quy tắc tính chu vi tam giác cân
Hình học luôn là một môn học khó nhằn với nhiều em học sinh bởi nó có khá nhiều công thức cần nhớ. Công thức tính chu vi tam giác cân chính là một công thức cơ bản bởi tam giác cân là một tam giác đặc biệt với 2 cạnh bằng nhau, điều này khiến cho việc tính chu vi tam giác dạng này trở nên dễ dàng hơn.
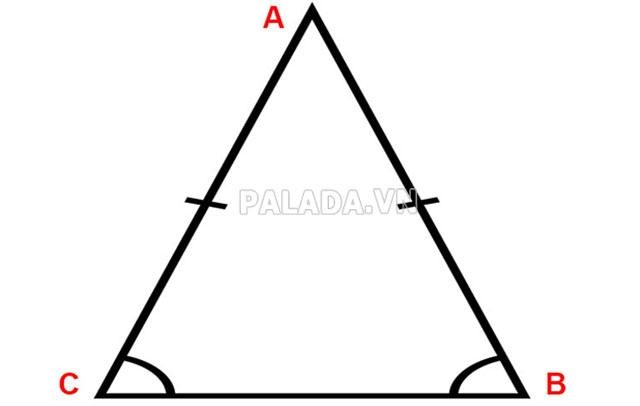
Chúng ta có ví dụ một tam giác cân ABC như hình trên, với 2 cạnh bên AB = AC.
Đối với một tam giác thường thì công thức tính chu vi của tam giác đó sẽ là:
P = AB + AC + BC
Nhưng do đây là tam giác cân có hai cạnh AB và AC bằng nhau nên chúng ta có thể rút gọn công thức này như sau:
P = AB * 2 + BC = AC * 2 + BC.
Quy tắc tính chu vi hình tam giác đều
Tam giác đều là loại tam giác đặc biệt nhất với độ dài ba cạnh bằng nhau và các góc có số đo bằng nhau là 60 độ, do vậy cách tính chu vi tam giác đều khá đơn giản.
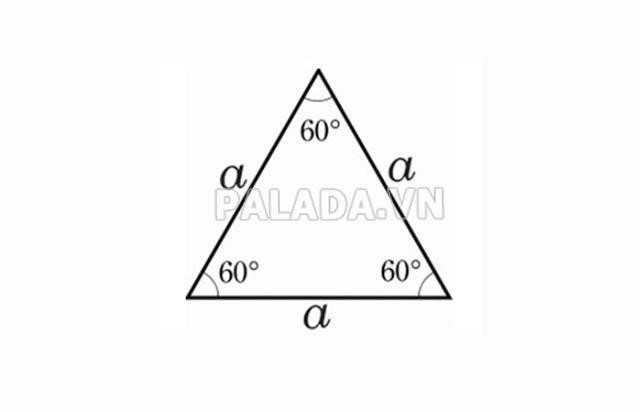
Cách tính chu vi tam giác đều so với quy tắc tính chu vi hình tam giác thông thường như thế nào? Nếu như chu vi tam giác thông thường bằng tổng độ dài ba cạnh thì chu vi hình tam giác đều được tính bằng công thức như sau:
P = a * 3
Trong đó: P là ký hiệu của chu vi.
a là độ dài cạnh tam giác đều.
Có thể phát biểu bằng lời: Muốn tính chu vi của tam giác đều, ta lấy độ dài của một cạnh nhân với 3.
* Cụ thể: Cho tam giác đều ABC với AB = AC = BC = 4 cm. Tính chu vi tam giác ABC.
Hướng dẫn: Các em chỉ cần áp dụng công thức tính chu vi của tam giác đều, ta có:
Chu vi tam giác đều ABC là:
P = 4 * 3 = 12 (cm)
* Hướng dẫn cách vẽ tam giác đều nhanh và chính xác nhất:
Để vẽ một tam giác đều ABC, các bạn thực hiện theo 3 bước đơn giản như sau:
– Bước 1: Vẽ cạnh BC có độ dài theo yêu cầu.
– Bước 2: Dùng compa vẽ cung tròn có tâm B, bán kính là BC và cung tròn có tâm C, bán kính là BC; hai cung tròn cắt nhau tại 1 điểm, gọi là điểm A.
– Bước 3: Nối điểm A với điểm B và điểm A với điểm C. Ta được tam giác đều ABC có độ dài các cạnh bằng nhau.
Thông qua bài viết trên, Palada.vn đã cùng các em học sinh và các bậc phụ huynh củng cố lại cách tính chu vi tam giác để có thể áp dụng vào bài tập môn toán cũng như trong thực tế. Nếu có bất kỳ thắc mắc nào các bạn hãy để lại bình luận bên dưới cho chúng mình nhé.



